Элементов.
 |
Рис. 2.7
Рассмотрим цепь, изображенную на рис.2.7. К этой цепи, состоящей из последовательно соединенных активного, индуктивного и емкостного элементов, подводится переменное напряжение U заданной частоты f. Рассчитаем эту цепь.
2.4.1. Последовательность расчета:
1) находим полное сопротивление (импеданс) участка цепи, содержащего последовательно соединенные элементы R, L, C
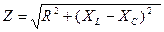 (2.15)
(2.15)
2) находим разность фаз тока и напряжения
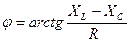 (2.16) Из формулы (2.15) следует, что можно моделировать cопротивление цепи в виде треугольника, у которого катеты равны R и (ХL-ХС), а гипотенуза равна полному сопротивлению Z.
(2.16) Из формулы (2.15) следует, что можно моделировать cопротивление цепи в виде треугольника, у которого катеты равны R и (ХL-ХС), а гипотенуза равна полному сопротивлению Z.
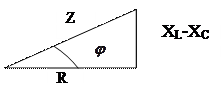 «Треугольник сопротивлений»:
«Треугольник сопротивлений»:
Угол между катетом R и гипотенузой Z соответствует разности фаз φ.
tgφ = 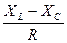 (2.17)
(2.17)
Из формулы (2.16) следуют частные случаи: разность фаз тока и напряжения:
· на активном элементе φR = 0;
· на идеальном индуктивном элементе φL= 900 ;
· на емкостном элементе φC= -900.
3) находим ток в цепи, используя закон Ома : I= 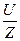
4) находим напряжения на отдельных элементах, также применяя закон Ома:
UR =I 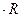 ; UL=I
; UL=I 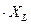 ; UC=I
; UC=I 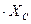 .
.
Примечание: Реальный индуктивный элемент является частным случаем рассмотренной выше цепи (последовательное соединение R и L, ХС=0)
В цепях переменного тока закон Ома выражается совокупностью соотношений:
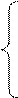 I =
I = 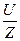
 (а)
(а)
(2.18)
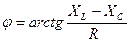 (б)
(б)
Соотношение (б) определяет разность фаз U и I.
Дата добавления: 2015-10-09; просмотров: 1185;
