Системы счисления. Перевод чисел из одной системы счисления в другую. Арифметические действия в системах счисления.
Система счисления (далее СС) - совокупность приёмов и правил для записи чисел цифровыми знаками.
Наиболее известна десятичная СС, в которой для записи чисел используются цифры 0,1,:,9. Способов записи чисел цифровыми знаками существует бесчисленное множество. Любая предназначенная для практического применения СС должна обеспечивать:
· возможность представления любого числа в рассматриваемом диапазоне величин;
· единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);
· простоту оперирования числами;
В зависимости от способов изображения чисел цифрами, системы счисления делятся на непозиционные и позиционные.
Непозиционной системой называется такая, в которой количественное значение каждой цифры не зависит от занимаемой ей позиции в изображении числа (римская система счисления).
Позиционной системой счисления называется такая, в которой количественное значение каждой цифры зависит от её позиции в числе (арабская система счисления). Количество знаков или символов, используемых для изображения числа, называется основанием системы счисления.
Позиционные системы счисления имеют ряд преимуществ перед непозиционными: удобство выполнения арифметических и логических операций, а также представление больших чисел, поэтому в цифровой технике применяются позиционные системы счисления.
Запись чисел может быть представлена в виде
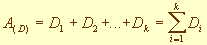 ,
,
где A(D) - запись числа A в СС D;Di - символ системы, образующие базу.
По этому принципу построены непозиционные СС.
В общем же случае системы счисления: A(B)=a1B1+a2B2 +...+anBn. Если положить, что Bi=q*Bi-1, а B1=1, то получим позиционную СС. При q=10 мы имеем дело с привычной нам десятичной СС.
На практике также используют другие СС:
| q | Название | Цифры |
| двоичная | 0,1 | |
| троичная | 0,1,2 | |
| восьмеричная | 0,...,7 | |
| шестнадцатеричная | 0,...,9,A, ...,F |
Каждая СС имеет свои правила арифметики (таблица умножения, сложения). Поэтому, производя какие-либо операции над числами, надо помнить о СС, в которой они представлены.
Если основание системы q превышает 10, то цифры, начиная с 10, при записи обозначают прописными буквами латинского: A,B,..., F. При этом цифре 10 соответствует знак 'A', цифре 11 - знак 'B' и т.д. В таблице ниже приводятся десятичные числа от 0 до 15 и их эквивалент в различных СС:
| десятичная | двоичная | восьмеричная | шестнадцатеричная |
| А | |||
| В | |||
| С | |||
| D | |||
| E | |||
| F | |||
В позиционной СС число можно представить через его цифры с помощью следующего многочлена относительно q:
A=a1*q0+a2*q1+...+an*qn (1)
Выражение (1) формулирует правило для вычисления числа по его цифрам в q-ичной СС. Для уменьшения количества вычислений пользуются т.н. схемой Горнера. Она получается поочерёдным выносом q за скобки:
A=(...((an*q+an-1)*q+an-2)*q+...)*q+a1
результат вычисления многочлена будет всегда получен в той системе счисления, в которой будут представлены цифры и основание и по правилам которой будут выполнены операции.
Правила перевода целых чисел
Результатом является целое число.
Из десятичной системы счисления - в двоичную и шестнадцатеричную:
a. исходное целое число делится на основание системы счисления, в которую переводится (2 или 16); получается частное и остаток;
b. если полученное частное не делится на основание системы счисления так, чтобы образовалась целая часть, отличная от нуля, процесс умножения прекращается, переходят к шагу в). Иначе над частным выполняют действия, описанные в шаге а);
c. все полученные остатки и последнее частное преобразуются в соответствии с таблицей в цифры той системы счисления, в которую выполняется перевод;
d. формируется результирующее число: его старший разряд - полученное последнее частное, каждый последующий младший разряд образуется из полученных остатков от деления, начиная с последнего и кончая первым. Таким образом, младший разряд полученного числа - первый остаток от деления, а старший - последнее частное.
Пример1. Выполнить перевод числа 19 в двоичную систему счисления:

Пример 2. Выполнить перевод числа 19 в шестнадцатеричную систему счисления:

Пример 3. Выполнить перевод числа 123 в шестнадцатеричную систему счисления:
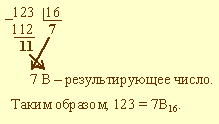
Из двоичной и шестнадцатеричной систем счисления - в десятичную. В этом случае рассчитывается полное значение числа по формуле.
Пример 4. Выполнить перевод числа 1316 в десятичную систему счисления. Имеем:
1316 = 1*161 + 3*160 = 16 + 3 = 19.
Таким образом, 1316 = 19.
Пример 5. Выполнить перевод числа 100112 в десятичную систему счисления. Имеем:
100112 = 1*24 + 0*23 + 0*22 + 1*21 + 1*20 = 16+0+0+2+1 = 19.
Таким образом, 100112 = 19.
Из двоичной системы счисления в шестнадцатеричную:
a. исходное число разбивается на тетрады (т.е. 4 цифры), начиная с младших разрядов. Если количество цифр исходного двоичного числа не кратно 4, оно дополняется слева незначащими нулями до достижения кратности 4;
b. каждая тетрада заменятся соответствующей шестнадцатеричной цифрой в соответствии с таблицей
Пример 6. Выполнить перевод числа 100112 в шестнадцатеричную систему счисления.
Поскольку в исходном двоичном числе количество цифр не кратно 4, дополняем его слева незначащими нулями до достижения кратности 4 числа цифр. Имеем:

В соответствии с таблицей 00112 = 112 = 316 и 00012 = 12 = 116.
Тогда 100112 = 1316.
Из шестнадцатеричной системы счисления в двоичную:
a. каждая цифра исходного числа заменяется тетрадой двоичных цифр в соответствии с таблицей. Если в таблице двоичное число имеет менее 4 цифр, оно дополняется слева незначащими нулями до тетрады;
b. незначащие нули в результирующем числе отбрасываются.
Пример 7. Выполнить перевод числа 1316 в двоичную систему счисления.
По таблице имеем: 116 = 12 и после дополнения незначащими нулями 12 = 00012; 316 = 112 и после дополнения незначащими нулями 112 = 00112. Тогда 1316 = 000100112. После удаления незначащих нулей имеем 1316 = 100112.
Правила перевода правильных дробей
Результатом является всегда правильная дробь.
Из десятичной системы счисления - в двоичную и шестнадцатеричную:
a. исходная дробь умножается на основание системы счисления, в которую переводится (2 или 16);
b. в полученном произведении целая часть преобразуется в соответствии с таблицей в цифру нужной системы счисления и отбрасывается - она является старшей цифрой получаемой дроби;
c. оставшаяся дробная часть вновь умножается на нужное основание системы счисления с последующей обработкой полученного произведения в соответствии с шагами а) и б).
d. процедура умножения продолжается до тех пор, пока ни будет получен нулевой результат в дробной части произведения или ни будет достигнуто требуемое количество цифр в результате;
e. формируется результат: последовательно отброшенные в шаге б) цифры составляют дробную часть результата, причем в порядке уменьшения старшинства.
Пример 8. Выполнить перевод числа 0,847 в двоичную систему счисления. Перевод выполнить до четырех значащих цифр после запятой.
Имеем:
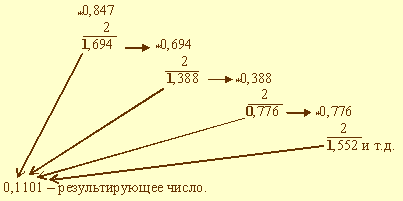
В данном примере процедура перевода прервана на четвертом шаге, поскольку получено требуемое число разрядов результата. Очевидно, это привело к потере ряда цифр.
Таким образом, 0,847 = 0,11012.
Пример 9. Выполнить перевод числа 0,847 в шестнадцатеричную систему счисления. Перевод выполнить до трех значащих цифр.
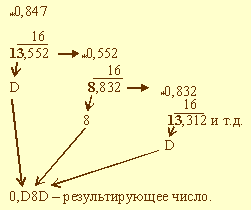
В данном примере также процедура перевода прервана. Таким образом, 0,847 = 0,D8D2.
Из двоичной и шестнадцатеричной систем счисления - в десятичную. В этом случае рассчитывается полное значение числа по формуле, причем коэффициенты ai принимают десятичное значение в соответствии с таблицей.
Пример 10. Выполнить перевод из двоичной системы счисления в десятичную числа 0,11012. Имеем:
0,11012 = 1*2-1 + 1*2-2 + 0*2-3 +1*2-4 = 0,5 + 0,25 + 0 + 0,0625 = 0,8125.
Расхождение полученного результата с исходным для получения двоичной дроби числом вызвано тем, что процедура перевода в двоичную дробь была прервана.
Таким образом, 0,11012 = 0,8125.
Пример 11. Выполнить перевод из шестнадцатеричной системы счисления в десятичную числа 0,D8D16. Имеем:
0,D8D16 = 13*16-1 + 8*16-2 + 13*16-3 = 13*0,0625 + 8*0,003906 + 13* 0,000244 = 0,84692.
Расхождение полученного результата с исходным для получения двоичной дроби числом вызвано тем, что процедура перевода в шестнадцатеричную дробь была прервана.
Таким образом, 0,D8D16 = 0,84692.
Из двоичной системы счисления в шестнадцатеричную:
a. исходная дробь делится на тетрады, начиная с позиции десятичной точки вправо. Если количество цифр дробной части исходного двоичного числа не кратно 4, оно дополняется справа незначащими нулями до достижения кратности 4;
b. каждая тетрада заменяется шестнадцатеричной цифрой в соответствии с таблицей.
Пример 12. Выполнить перевод из двоичной системы счисления в шестнадцатеричную числа 0,11012. Имеем:
0,11012 = 0,11012 В соответствии с таблицей 11012 = D16. Тогда имеем 0,11012 = 0,D16.
Пример 13. Выполнить перевод из двоичной системы счисления в шестнадцатеричную числа 0,00101012.
Поскольку количество цифр дробной части не кратно 4, добавим справа незначащий ноль: 0,00101012 = 0,001010102. В соответствии с таблицей 00102 = 102 = 216 и 10102 = A16. Тогда имеем 0,00101012 = 0,2A16.
Из шестнадцатеричной системы счисления в двоичную:
a. каждая цифра исходной дроби заменяется тетрадой двоичных цифр в соответствии с таблицей;
b. незначащие нули отбрасываются.
Пример 14. Выполнить перевод из шестнадцатеричной системы счисления в двоичную числа 0,2А16.
По таблице имеем 216 = 00102 и А16 = 10102. Тогда 0,2А16 = 0,001010102.
Отбросим в результате незначащий ноль и получим окончательный результат: 0,2А16 = 0,00101012.
Правило перевода дробных чисел
Отдельно переводится целая часть числа, отдельно - дробная. Результаты складываются.
Пример 15. Выполнить перевод из десятичной системы счисления в шестнадцатеричную числа 19,847. Перевод выполнять до трех значащих цифр после запятой.
Представим исходное число как сумму целого числа и правильной дроби:
19,847 = 19 + 0,847.
Как следует из примера 3.2, 19 = 1316; а в соответствии с примером 3.9 0,847 = 0,D8D16. Тогда имеем:
19 + 0,847 = 1316 + 0,D8D16 = 13,D8D16.
Таким образом, 19,847 = 13,D8D16. Правила выполнения простейших арифметических действий.
Правила сложения
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево. Таблицы сложения:
Сложение в двоичной системе
| + | ||
Сложение в восьмеричной системе
| + | ||||||||
Сложение в шестнадцатеричной системе
| + | A | B | C | D | E | F | ||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | A | B | C | D | E | F | ||||||||||
| B | B | C | D | E | F | 1A | ||||||||||
| C | C | D | E | F | 1A | 1B | ||||||||||
| D | D | E | F | 1A | 1B | 1C | ||||||||||
| E | E | F | 1A | 1B | 1C | 1D | ||||||||||
| F | F | 1A | 1B | 1C | 1D | 1E |
Пример 16. Сложить двоичные числа 11012 и 110112.
Запишем слагаемые в столбик и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов:
5 4 3 2 1
+ 1 1 0 1
1 1 0 1 1
Процесс образования результата по разрядам описан ниже:
a. разряд 1 формируется следующим образом: 1 + 1 = 10; 0 остается в разряде 1, 1 переносится во второй разряд;
b. разряд 2 формируется следующим образом: 0 + 1 + 1 = 10, где вторая 1 - единица переноса; 0 остается в разряде 2, 1 переносится в третий разряд;
c. третий разряд формируется следующим образом: 1 + 0 + 1 = 10, где вторая 1 - единица переноса; 0 остается в разряде 3, 1 переносится в разряд 4;
d. четвертый разряд формируется следующим образом: 1 + 1 + 1 = 11, где третья 1 - единица переноса; 1 остается в разряде 4, 1 переносится в пятый разряд;
e. пятый разряд формируется следующим образом: 1 + 1 = 10; где вторая 1 - единица переноса; 0 остается в разряде 5, 1 переносится в шестой разряд.
Таким образом:
1 1 0 1
+ 1 1 0 1 1
1 0 1 0 0 0
Проверим результат. Для этого определим полные значения слагаемых и результата:
11012 = 1*23 +1*22 + 0*21 + 1*20 = 8 + 4 + 1 = 13;
110112 = 1*24 + 1*23 + 0*22 + 1*21 + 1*20 = 16 + 8 + 2 + 1 = 27;
1010002 = 1*25 + 0*24 + 1*23 + 0*22 + 0*21 + 0*21 = 32 + 8 = 40.
Поскольку 13 + 27 = 40, двоичное сложение выполнено верно.
Пример 17. Сложить шестнадцатеричные числа 1С16 и 7В16.
Запишем слагаемые в столбик и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов:
2 1
+ 1 С
7 В
Процесс образования результата по разрядам описан ниже (он включает преобразование в процессе сложения каждой шестнадцатеричной цифры в десятичное число и обратные действия):
a. разряд 1 формируется следующим образом: С16 + В16 = 12 + 11 = 23 = 1716; 7 остается в разряде 1; 1 переносится в разряд 2;
b. разряд 2 формируется следующим образом: 116 + 716 + 116 = 916, где вторая 116 - единица переноса.
Таким образом:
1 С
+ 7 В
9 7
Проверим результат. Для этого определим полные значения слагаемых и результата:
1С16 = 1*161 + 12*160 = 16 + 12 = 28;
7В16 = 7*161 + 11*160 = 112 + 11 = 123;
9716 = 9*161 + 7*160 = 144 + 7 = 151.
Поскольку 28 + 123 = 151, сложение выполнено верно.
Дата добавления: 2015-10-09; просмотров: 861;
