Дисперсия света

Дисперсией света называется зависимость показателя преломления вещества от частоты (длины волны) света или зависимость фазовой скорости световых волн от его частоты. Дисперсия света представляется в виде зависимости

n = f(λ). (29.1)

Следствием дисперсии является разложение в спектр пучка белого света при прохождении его через призму.

Рассмотрим дисперсию света в призме (рис.29.1). Пусть монохроматический пучок света падает на призму с преломляющим углом А и показателем преломления n под углом α₁. После двухкратного преломления (на левой и правой гранях призмы) луч оказывается отклоненным от первоначального направления на угол φ. Получено: Рис.29.1.

φ = А (n-1), (29.2)

т.е. угол отклонения лучей призмой тем больше, чем больше преломляющий угол призмы. Угол отклонения лучей призмой зависит от величины (n-1), а n- функция длины волны, поэтому лучи разных длин волн после прохождения призмы окажутся отклоненными на разные углы, т.е. пучок белого света за призмой разлагается в спектр.

С помощью призмы, так же как и с помощью дифракционной решетки, разлагая свет в спектр, можно определить его спектральный состав.

Величина D =dn/dλ, (29.3)

называемая дисперсией вещества, показывает, как быстро изменяется показатель преломления с длиной волны. Показатель преломления для прозрачных веществ с уменьшением длины волны увеличивается; следовательно, величина dn/dλ по модулю также увеличивается с уменьшением λ. Такая дисперсия называется нормальной. А вблизи линий и полос поглощения будет иным: n уменьшается с уменьшением λ. Такой ход зависимости n от λ называется аномальной дисперсией.

Из электромагнитной теории Максвелла следует, что абсолютный показатель преломления среды

n = 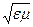, (29.4)

где ε – диэлектрическая проницаемость среды, μ – магнитная проницаемость. В оптической области спектра для всех веществ μ~1, поэтому n = . Выявляются некоторые противоречия с опытом: величина n, являясь переменной, остается в то же время определенной постоянной . Значения n, получаемые из этого выражения, не согласуются с опытными данными. Трудности объяснения дисперсии света с точки зрения электромагнитной теории Максвелла устраняются электронной теорией Лоренца. В электронной теории дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле волны.

Применим электронную теорию дисперсии света для однородного диэлектрика, предположив, что дисперсия света является следствием зависимости ε от частоты ω световых волн. Диэлектрическая проницаемость веществ по определению равна

ε =1+Р/( ε₀Е), (29.5)

где ε₀ – электрическая постоянная, Р- мгновенное значение поляризованности, Е-вектор напряженности. Тогда

n² =1+Р/( ε₀Е), (29.6)

т.е. зависит от Р. В данном случае основное значение имеет электронная поляризация, т.е. вынужденные колебания электронов под действием электрической составляющей поля волны.

В первом приближении можно считать, что вынужденные колебания совершают только внешние, наиболее слабо связанные с ядром электроны- оптические электроны.

Для простоты рассмотрим колебания только одного оптического электрона. Наведенный дипольный момент электрона, совершающего колебания, равен

р=ех, (29.7)

где е-заряд электрона, х- смещение электрона под действием электрического поля световой волны. Тогда мгновенное значение поляризованности

Р=ех n₀, (29.8)

n₀ – концентрация электронов. Получим

n² =1+е х n₀/( ε₀Е). (29.9)

Следовательно, задача сводится к определению смещения х электрона под действием внешнего поля Е.

Уравнение вынужденных колебаний электрона (без учета силы сопротивления) запишется в виде

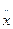+ ω₀²x = (F₀/m) соsωt = (еЕ₀/m) соsωt, (29.10)

где F₀ = еЕ₀ –амплитудное значение силы, действующей на электрон со стороны поля волны, ω₀ – собственная частота колебаний электрона, m –масса электрона.

Решив это уравнение найдем зависимость n² = ε от констант атома и ω-частоты внешнего поля

Решение уравнения можно записать в виде:

х = А соsωt, (29.11)

где А = 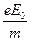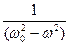. (29.12)

Подставим в уравнение (29.10) вместо х уравнения (29.11) и (29.12). Получим

n² = 1+ 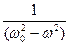. (29.12)

Если в веществе имеются различные заряды e_i, совершающие вынужденные колебания с различными собственными частотами ω_0i, то

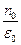
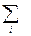
n² = 1+ 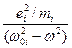, (29.13)

где m_i – масса i –го заряда.

29.3. Естественный и поляризованный свет

Следствием теории Максвелла, является поперечность световых волн: векторы напряженностей электрического Е и магнитного Н полей волны взаимно перпендикулярны и колеблются перпендикулярно вектору скорости V распространения волны. Поэтому для описания закономерностей поляризации света достаточно знать поведение лишь одного из векторов. Обычно все рассуждения ведутся относительно светового вектора — вектора напряженности Е электрического поля (это название обусловлено тем, что при действии света на вещество основное значение имеет электрическая составляющая поля волны, действующая на электроны в атомах вещества).

Свет представляет собой суммарное электромагнитное излучение множества атомов. Атомы же излучают световые волны независимо друг от друга, поэтому световая волна, излучаемая телом в целом, характеризуется всевозможными равновероятными колебаниями светового вектора. Свет со всевозможными равновероятными ориентациями вектора Е (и, следовательно, Н) называется естественным.

Свет, в котором направления колебаний светового вектора каким-то образом упорядочены, называется поляризованным. Так, если в результате каких-либо внешних воздействий появляется преимущественное (но не исключительное) направление колебаний вектора Е, то имеем дело с частично поляризованным светом. Свет, в котором вектор Е (и, следовательно, Н) колеблется только в одном направлении, перпендикулярном лучу, называется плоскополяризованным (линейно поляризованным).

Плоскость, проходящая через направление колебаний светового вектора плоскополяризованной волны и направление распространения этой волны, называется плоскостью поляризации.

Степенью поляризации называется величина

Р= 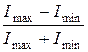, (29.14)

где І_mаx и І_min — соответственно максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором. Для естественного света І_mаx = І_min и Р=0, для плоскополяризованного І_min =0 и Р=1.

Степень поляризации степень выделения световых волн с определенной ориентацией электрического (и магнитного) вектора) зависит от угла падения лучей и показателя преломления.

Естественный свет можно преобразовать в плоскополяризованный, используя так называемые поляризаторы, пропускающие колебания только определенного направления. В качестве поляризаторов могут быть использованы среды, анизотропные в отношении колебаний вектора Е, например кристаллы. Из природных кристаллов - турмалин.

Рассмотрим классические опыты с турмалином (рис.29.2). Направим естественный свет перпендикулярно пластинке турмалина Т₁, вырезанной параллельно так называемой оптической оси ОО'. Вращая кристалл Т₁ вокруг направления луча никаких изменений интенсивности прошедшего через турмалин света не наблюдаем. Если на пути луча поставить вторую пластинку турмалина Т₂ и вращать ее вокруг направления луча, то интенсивность света, прошедшего через пластинки, меняется в зависимости от угла a (рис.29.3) между оптическими осями кристаллов по закону Малюса:

Рис.29.3.

I = I₀соs² a , (29.15)

где I₀ и I — соответственно интенсивности света, падающего на второй кристалл и вышедшего из него. Следовательно, интенсивность прошедшего через пластинки света изменяется от минимума (полное гашение света) при a=π/2 (оптические оси пластинок перпендикулярны) до максимума при a= 0 (оптические оси пластинок параллельны).

Результаты опытов с кристаллами турмалина объясняются довольно просто. Первая пластинка турмалина пропускает колебания только определенного направления (на рис. это направление показано стрелкой АВ), т.е. преобразует естественный свет в плоскополяризованный. Вторая пластинка турмалина в зависимости от ее ориентации из поляризованного света пропускает большую или меньшую его часть. На рис. обе пластинки расположены так, что направления пропускаемых ими колебаний АВ и А'В' перпендикулярны друг другу. В данном случае Т₁ пропускает колебания, направленные по АВ, а Т₂ их полностью гасит, т. е. за вторую пластинку турмалина свет не проходит.

Пластинка Т₁, преобразующая естественный свет в плоскополяризованный, является поляризатором. Пластинка Т₂, служащая для анализа степени поляризации света, называется анализатором. Обе пластинки совершенно одинаковы (их можно поменять местами).

Если естественный свет падает на границу раздела двух диэлектриков (например, воздуха и стекла), то часть его отражается, а часть преломляется и распространяется во второй среде. Устанавливая на пути отраженного и преломленного лучей анализатор (например, турмалин), убеждаемся в том, что отраженный и преломленный лучи частично поляризованы: при поворачивании анализатора вокруг лучей интенсивность света периодически усиливается и ослабевает (полного гашения не наблюдается).

Степень поляризации зависит от угла падения лучей и показателя преломления. Д. Брюстер установил закон, согласно которому при угле падения i_В (угол Брюстера), определяемого соотношением

tgi_В = n₂₁, (29.16)

(п₂₁ — относительный показатель преломления второй среды относительно первой), отраженный луч является плоскополяризованным (содержит только колебания, перпендикулярные плоскости падения) (рис.29.4). Преломленный же луч при угле падения i_В поляризуется Рис.29.4.

максимально, но не полностью.