Теплоемкость. Удельная теплоемкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:

Удельная теплоемкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:

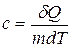. (11.9)

Единица удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кг×К)).

Молярная теплоемкость – величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:

C_m= 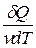,(11.10)

где: v=m/M — количество вещества.

Единица молярной теплоемкости — джоуль на моль·кельвин (Дж/(моль·К)). Удельная теплоемкость с связана с молярной С_m соотношением

С_m = сМ,(11.11)

Различают молярные теплоемкости при постоянном объеме С_Vи постоянном давлении С_р, если в процессе нагревания вещества его объем или давление поддерживается постоянным.

Запишем выражение первого начала термодинамики (11.6) для 1 моль газа

C_mdT = dU_m + pdV_m.(11.12)

Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю (см. 11.7) и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии:

С_V= 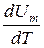,(11.13)

т. е. молярная теплоемкость газа при постоянном объеме С_V равна изменению внутренней энергии 1 моль газа при повышении его температуры на 1 К

C_V =iR/2. (11.14)

Если газ нагревается при постоянном давлении, то выражение (11.12) можно запи­сать в виде

C_V = .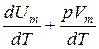

Учитывая, что 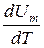не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от р, ни от V, а определяется лишь температурой Т)и всегда равна C_V , дифференцируя уравнение Клапейрона - Менделеева pV_m=RT по Τ (р=const),получаем

С_p = С_V+R. (11.15)

Выражение (11.15) называется уравнением Майера; оно показывает, что С_р всегда больше С_V на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Использовав (11.14), выражение (11.15) можно записать в виде:

С_p= 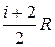.(11.16)

При рассмотрении термодинамических процессов важно знать характерное для каждого газа отношение С_р к С_V:

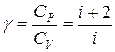. (11.17)

Из формул следует, что молярные теплоемкости определяются лишь числом степеней свободы и не зависят от температуры. Это утверждение молекулярно-кинетической теории справедливо в довольно широком интервале температур лишь для одноатомных газов. Уже у двухатомных газов число степеней свободы, проявляющееся в теплоемкости, зависит от температуры. Молекула двухатомного газа обладает тремя поступательными, двумя вращательными и одной колебательной степенями свободы.

По закону равномерного распределения энергии по степеням свободы, для комнатных температур C_V=⁷/₂R. Из качественной экспериментальной зависимости молярной теплоемкости С_V водорода (рис.11.4) следует, что оназависит от температуры: при низкой температуре (ниже 50 К) C_V =¹/₂ R,при

Рис.11.4 комнатной — C_V = ³/₂R (вместо расчетных ⁷/₂ R) и при очень высокой — С_V = ⁷/₂ R. Это можно объяснить, предположив, что при низких температурах наблюдается только поступательное движение молекул, при комнатных — добавляется их вращение, а при высоких — к этим двум видам движения добавляются еще и колебания молекул.