Упрощенный метод определения эксергетического КПД сложной термодинамической системы

Введем понятие эксергии теплового потока.

Эксергия теплового потока Е_q при температуре Т определяется количеством работы, которое может быть получено или должно быть затрачено в обратимом процессе переноса энтропии, характеризующей данный тепловой поток, на уровень температуры окружающей среды. Эта термодинамическая функция характеризует не энергию теплового потока, а его максимально возможную работу, которую этот поток может совершить вне рассматриваемой системы. Следует подчеркнуть, что возможная работа теплового потока не является материальной величиной, поэтому для нее закон сохранения энергии не справедлив. Однако учет потерь от необратимости процессов (эксергетических потерь) позволяет составлять ее баланс и, следовательно, открывает возможность определения эксергетического КПД.

Математическое выражение для эксергии теплового потока в условиях изобарического процесса 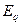может быть представлено в виде:

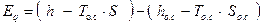. (5.1)

Выразим приращение энтропии через среднетермодинамическую температуру потока Т^Т:

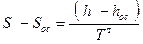, (5.2)

тогда:

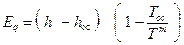. (5.3)

Одним из основных параметров в расчетах по определению эксергетического КПД теплопередачи является среднетермодинамическая температура нагрева (охлаждения) материальных потоков в процессе их энергетического взаимодействия. Среднетермодинамическая температура равна отношению изменения (приращения) энтальпии нагреваемого (охлаждаемого) потока к соответствующему приращению энтропии этого потока.

Определим эксергетический КПД сложной теплоиспользующей схемы и установления связи между эксергетическим КПД ее элемента с эксергетическим КПД сложной теплоиспользующей схемы в привычных для пользователя параметрах.

Для вычисления эксергетического КПД сложной тепловой схемы примем следующие соотношения:

Удельный тепловой поток, переданный (воспринятый) в
i -ом теплообменнике:

q_i = DQ _i / Σ ΔQ _i , (5.4)

где DQ_i – тепловой поток, переданный (воспринятый) в
i -ом теплообменнике; ΣΔQ_i – сумма тепловых потоков, переданных (воспринятых) по всем элементам рассматриваемой системы.

Приведенный тепловой поток для i- го теплообменного аппарата:

- нагреваемый поток: q_{пр.н =} q_i / 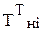, (5.5) охлаждаемый поток: q_пр.о = q_i / 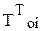, (5.6)

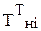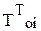где и – соответственно среднетермодинамическая температура нагреваемой и охлаждаемой среды для i- го теплообменного аппарата.

В большинстве практических случаев при термодинамическом анализе тепловых схем технологических процессов среднетермодинамическая температура отдельных потоков Т^Т может быть выражена через их истинные температуры следующими приближенными формулами:

- для процессов без фазовых превращений: Т^Т ≈ (Т_н + Т_к) /2 ; (5.7)

- для процессов при фазовом переходе первого рода: Т^Т ≈ Т_s, (5.8)

где Т_н и Т_к — температуры потока в начале и конце теплового процесса;
Т_s — температура фазового перехода.

Как известно, эксергетический КПД сложной тепловой схемы 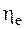можно вычислить из уравнения:

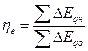, (5.9) где 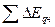и 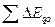- сумма приращений эксергий всех нагреваемых и охлаждаемых потоков, соответственно.

Раскроем числитель и знаменатель через значения для единичного теплообменного аппарата по формуле:

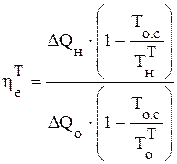, (5,10)

где ∆Q_н, ∆Q_о - тепловые потоки нагреваемой и охлаждаемой среды соответственно; Т_о.с – температура окружающей среды (для большинства случаев, встречающихся на практике можно принять 300 К).

Тогда с учетом (3.30-3.31) не трудно получить эксергетический КПД для сложной адиабатической тепловой схемы в виде:

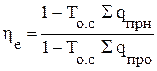. (5,11)

Найдем связь между эксергетическим КПД элемента 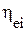с эксеретическим КПД в целом тепловой схемы 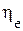, куда входит этот элемент. Доля затраченной эксергии в i-ом элементе γ_i к общей эксергии, затраченной в схеме:

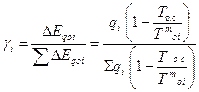. (5.12)

Тогда общий КПД тепловой схемы можно вычислить:

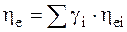. (5.13)