Оценка и управление точностью металлообрабатывающего технологического процесса.
Данный вопрос обстоятельно рассматривается в курсе «Технология машиностроения». Здесь мы проводим краткое его изложение, т.к. рассмотренные здесь представления понадобятся при дальнейших рассуждениях.
В процессе массового, крупносерийного и даже единичного производства применяется статистический контроль точности и ее важнейшего звена размерной точности изделий. На основе сбора и анализа статистических данных осуществляются контроль и управление этим процессом.
В силу различных причин при обработке деталей нельзя два раза подряд получить один и тот же размер. Размер колеблется около некоторого среднего значения, обеспечиваемого настройкой. Погрешности, влияющие на колебание размера, делятся на систематические и случайные.
Учет и статистическая обработка этих погрешностей позволяют оценивать точность системы СПИД или всего технологического процесса и управлять этой точностью.
Многочисленные исследования показали, что рассеивание размеров от случайных погрешностей подчиняется закону нормального распределения (рис. 96).
Кривая Гуасса характерна тем, что она является однопараметрической кривой. Этим единственным параметром, определяющим вид кривой, является δ — среднее квадратичное отклонение.
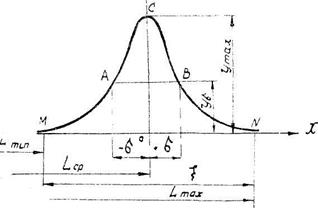
Рис. 9.1. Кривая нормального распределения.
На рис. 9.1 изображены наиболее типичные точки этой кривой. По оси X откладываются величины размеров (или их отклонение от среднего размера Lср — точки 0). По оси У откладывается частота попадания размеров на данное значение абсциссы (или интервал h).
Как известно, кривая Гаусса описывается следующим уравнением:
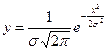
Точка С соответствует наибольшей частоте попадания размера, равной:
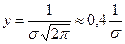
Точки А и В являются точками перегиба кривой и расположены от центра рассеяния на расстоянии ± σ. Частота У в точках А и В будет равна
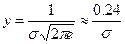
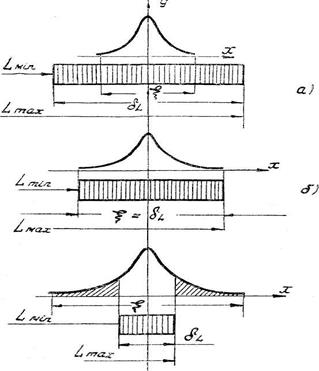
Рис. 9.2. Три случая взаимосвязи рассеивания размеров с допусками на эти размеры.
Точки М и N соответствуют практически точной величине поля рассеивания ξ.
ξ = 6σ = Lmax - Lmin
где
Lmin — минимальный размер, полученный из опыта;
Lmах — максимальный размер, полученный из опыта.
Расчеты показали, что в области x = ±0,36 σ находится 35% всех наблюденных значений (измеренных или изготовленных размеров); в области х = ±0,76 σ находится 50% всех наблюденный значений; и в области х = ±3 σ находится 99,7% всех наблюденных значений. Это обстоятельство и используется для оценки и управления точностью.
При оценке соответствия размерной точности изготавливаемого изделия той точности, которую обеспечивает технологический процесс, возможны 3 случая, изображенные на рис. 9.2.
На рис 9.2а изображен 1-й случай, когда поле рассеивания, обеспечиваемое технологическим процессом ξ = 6σ много меньше допуска на выполняемый размер δL.
В этом случае технологический процесс (станок, автоматическая линия, поточная линия и т.д.) будет устойчиво обеспечивать установленную размерную точность. При этом настройка может быть не очень точной.
Настроечный размер Lн будет равен Lср.
На рис. 9.2б приведен тот случай, когда поле допуска па заданный размер равно полю рассеивания, которое дает технологический процесс. Теоретически данный случай должен обеспечить годную продукцию, однако учитывая, что настроечный размер нельзя будет установить с нулевым допуском, придется считаться с вероятностью появления небольшого количества негодных деталей. Ожидаемое количество негодных деталей в зависимости от неточности настройки можно определить расчетом.
На рис. 9.2в приведен третий случай, когда поле рассеивания, обеспечиваемое технологическим процессом, существенно больше поля, заданного допуском. В этом случае технологический процесс для заданной точности будет нестабильным. Количество негодных деталей в процентах будет определено площадью заштрихованной части кривой.
В данном случае необходимо либо рассмотреть возможность расширения поля допуска, либо провести изучение и устранение причин рассеивания размеров, либо разработать новый более точный технологический процесс.
Таким образом, в случае нормального закона распределения погрешностей размерной обработки оценкой точности и стабильности техпроцесса может быть принята величина среднеквадратичного отклонения σ. Чем она меньше, тем точнее технологический процесс (станок, системы станков и т.д.) Все вышеприведенные рассуждения сделаны для случая совмещения центра поля рассеяния с срединой поля допуска.
Дата добавления: 2015-10-05; просмотров: 726;
