Int Fib ( int n )

{

if ( n == 0 ) return 0;

if ( n == 1 ) return 1;

return Fib(n-1) + Fib(n-2);

}

Заметим, что каждый рекурсивный вызов при n > 1порождает еще 2 вызова функции, многие выражения (числа Фибоначчи для малых n) вычисляются много раз. Поэтому практического значения этот алгоритм не имеет, особенно для большихn. Схема вычисления Fib(5)показана в виде дерева ниже:

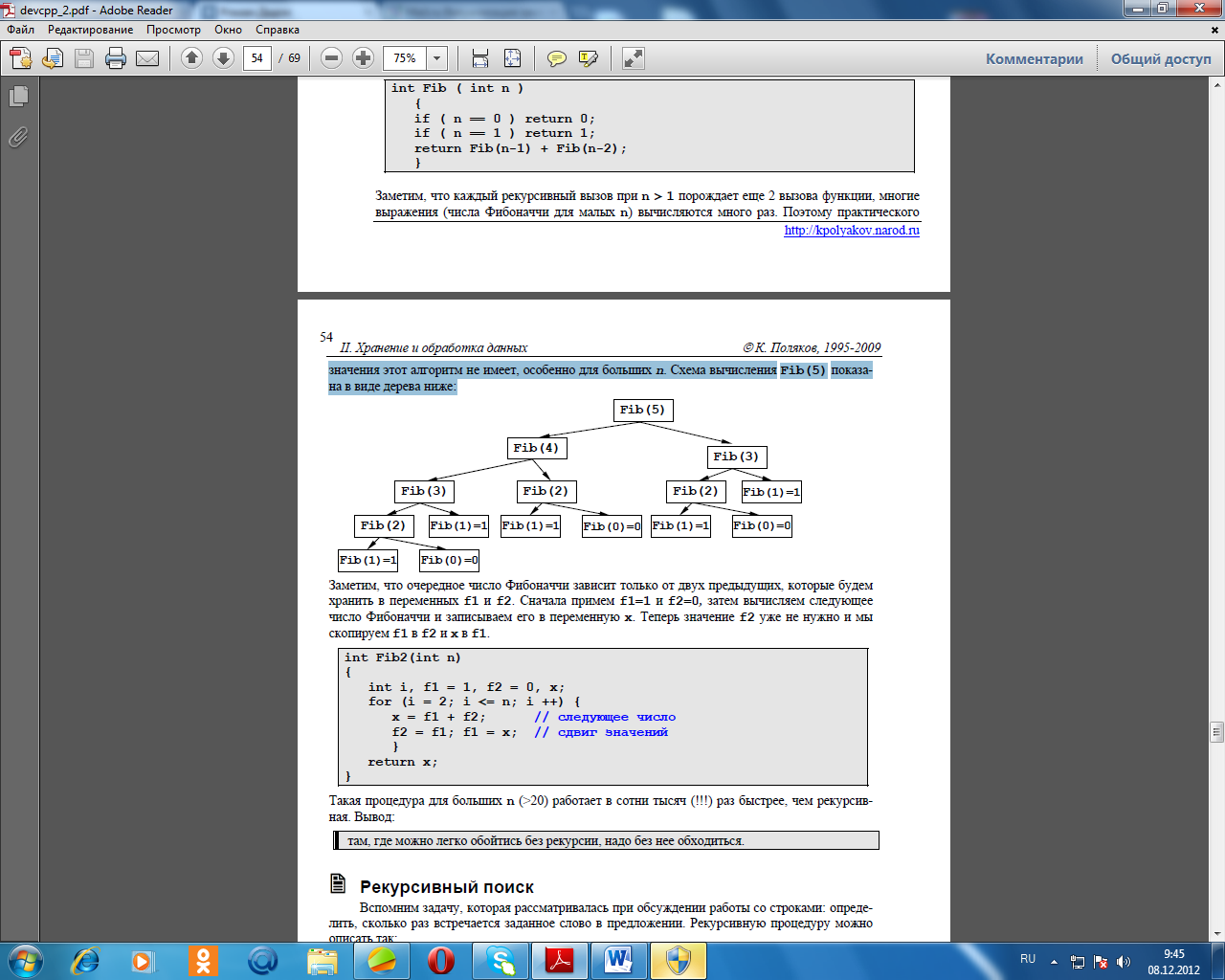
Заметим, что очередное число Фибоначчи зависит только от двух предыдущих, которые будем хранить в переменных f1и f2. Сначала примем f1=1и f2=0, затем вычисляем следующее число Фибоначчи и записываем его в переменную x. Теперь значение f2уже не нужно и мы скопируем f1в f2и xв f1.