Динамические свойства ДНВ при питании от источника напряжения.
Воспользуемся системой уравнений:
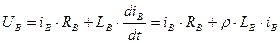
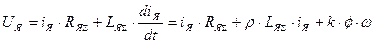
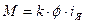
Перепишем эту систему в виде:

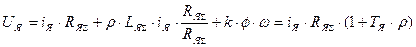
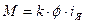
Здесь 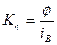 - коэффициент, соответствующий линейной части кривой намагничивания;
- коэффициент, соответствующий линейной части кривой намагничивания; 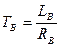 ;
; 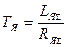 - электромагнитные постоянные цепи возбуждения и якорной цепи.
- электромагнитные постоянные цепи возбуждения и якорной цепи.
 Этим уравнениям соответствует приведенная ниже структурная схема. На ней даны два канала управления – канал управления потоком двигателя, которому соответствует управляющее воздействие UB и канал управления по цепи якоря с управляющим воздействием UЯ.
Этим уравнениям соответствует приведенная ниже структурная схема. На ней даны два канала управления – канал управления потоком двигателя, которому соответствует управляющее воздействие UB и канал управления по цепи якоря с управляющим воздействием UЯ.
Из схемы следует, что при отсутствии реакции якоря при UB=const и 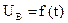 процессы в цепи возбуждения протекают независимо от процессов в якорной цепи, а процессы в последней зависят от изменения Ф.
процессы в цепи возбуждения протекают независимо от процессов в якорной цепи, а процессы в последней зависят от изменения Ф.
Цепь возбуждения представляет собой апериодическое звено с постоянной времени ТВ, которая для двигателей от нескольких кВт до нескольких тысяч кВт находится в пределах (0,2¸5,0)с. Индуктивность ее можно определить по формуле.
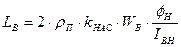 Гн или
Гн или 
 Здесь WB – число витков обмотки возбуждения на одном полюсе;
Здесь WB – число витков обмотки возбуждения на одном полюсе; 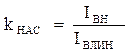 - коэффициент насыщения, а IB.ЛИН – ток возбуждения, создающий номинальный поток Фн при отсутствии насыщения магнитной цепи (см. рис.)
- коэффициент насыщения, а IB.ЛИН – ток возбуждения, создающий номинальный поток Фн при отсутствии насыщения магнитной цепи (см. рис.)
При работе на насыщенной части кривой намагничивания LB и ТВ уменьшаются, причем 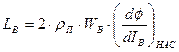 . Изменение Ф вносят нелинейность в математическое описание процессов преобразования энергии, поэтому структурная схема, изображенная на рис., используется для анализа динамических свойств эл.привода с ДНВ на ЭВМ.
. Изменение Ф вносят нелинейность в математическое описание процессов преобразования энергии, поэтому структурная схема, изображенная на рис., используется для анализа динамических свойств эл.привода с ДНВ на ЭВМ.
Обычно при питании от источника напряжения ДНВ работает при Ф=ФН=const. При этом уравнение динамической механической характеристики имеет вид
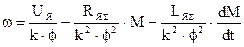 , откуда
, откуда
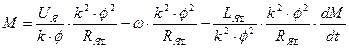 , или
, или
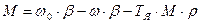 ; или
; или 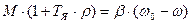
Этому уравнению соответствует структурная схема.
 Она показывает, что при Ф=const ЭМП с независимым возбуждением представляет собой апериодическое звено с постоянной времени ТЯ. Индуктивность рассеяния якорной цепи двигателя может быть вычислена по приближенной формуле Уманского – Линвилля.
Она показывает, что при Ф=const ЭМП с независимым возбуждением представляет собой апериодическое звено с постоянной времени ТЯ. Индуктивность рассеяния якорной цепи двигателя может быть вычислена по приближенной формуле Уманского – Линвилля.
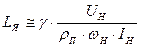 , где
, где
g=0,5¸0,6 для некомпенсированных машин и g=0,25 для компенсированных машин.
ТЯ для двигателей средней и большей мощности равно (0,02¸0,1)с, причем наибольшее значение соответствует некомпенсированным, либо тихоходным двигателям.
ДНВ имеет бесконечно большое число динамических характеристик, соответствующих динамическим процессам, зависящим от вида механической части, начальных условий, характера управляющих и возмущающих воздействий. По ним можно судить о свойствах как самого ДНВ, так и механической части. Поэтому для анализа динамических свойств самого двигателя их использовать нельзя.
В установившихся динамических режимах, например, при наличии периодической составляющей нагрузки эл.привода, динамическая механическая характеристика для каждого цикла установившихся колебаний одинакова и форма ее зависит только от электромеханических свойств двигателя. Установим, какой вид динамическая механическая характеристика имеет в этом случае. Пусть момент двигателя в установившемся динамическом режиме изменяется по закону 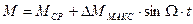 .
.
Тогда согласно вышеприведенному выражению:
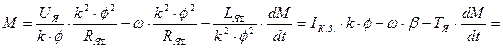
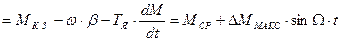 ,
,
откуда после нахождения производной 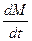 определим w:
определим w:
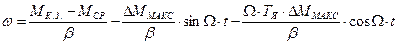 , или
, или
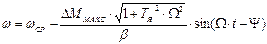 ,
,
где 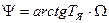 .
.
Изобразив на графике статическую характеристику (1), кривые 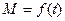 и
и 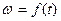 , задаваясь разными значениями времени t, на фоне статической характеристики можно построить динамическую характеристику. Это замкнутая кривая (2). Она существенно отличается от статической и отклонение ее от статической объясняется влиянием электромагнитной инерции якорной цепи. Уменьшение частоты W вынужденных колебаний или снижение ТЯ уменьшают эти отклонения. В пределе при W®0 или ТЯ®0 динамическая характеристика сольется со статической.
, задаваясь разными значениями времени t, на фоне статической характеристики можно построить динамическую характеристику. Это замкнутая кривая (2). Она существенно отличается от статической и отклонение ее от статической объясняется влиянием электромагнитной инерции якорной цепи. Уменьшение частоты W вынужденных колебаний или снижение ТЯ уменьшают эти отклонения. В пределе при W®0 или ТЯ®0 динамическая характеристика сольется со статической.
 Если с помощью структурной схемы, изображенной ранее, определить передаточную функцию динамической жесткости механической характеристики, она будет иметь вид:
Если с помощью структурной схемы, изображенной ранее, определить передаточную функцию динамической жесткости механической характеристики, она будет иметь вид:
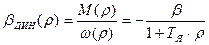
Заменив r на j×W, получим выражения амплитудно-частотной и фазочастотной характеристик динамической жесткости.
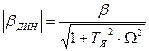 :
: 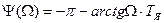
 Соответствующие им кривые приведены на рис. Из них видно, что электромагнитная инерция приводит к уменьшению модуля динамической жесткости тем в большей степени, чем выше W. Одновременно сдвиг по фазе между колебаниями w и М изменяется от 180°, соответствующих статической жесткости (W=0) до 90° при W® к бесконечности.
Соответствующие им кривые приведены на рис. Из них видно, что электромагнитная инерция приводит к уменьшению модуля динамической жесткости тем в большей степени, чем выше W. Одновременно сдвиг по фазе между колебаниями w и М изменяется от 180°, соответствующих статической жесткости (W=0) до 90° при W® к бесконечности.
Введение добавочного сопротивления в цепь якоря ДНВ уменьшает ТЯ. При этом если в пределах возможных частот колебаний 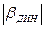 снижается незначительно, а y остается близким к 180°, то можно без существенных погрешностей исследовать динамические процессы пользуясь выражением статической механической характеристики.
снижается незначительно, а y остается близким к 180°, то можно без существенных погрешностей исследовать динамические процессы пользуясь выражением статической механической характеристики.
Отметим в заключение, что проведенный анализ динамических свойств ЭМП независимого возбуждения справедлив полностью только для компенсированных двигателей.
Математическое описание процессов электромеханического преобразования энергии в двигателе постоянного тока последовательного возбуждения (ДПВ)
 У двигателя последовательного возбуждения обмотка возбуждения включена последовательно с обмоткой якоря и его поток Ф является функцией тока якоря, т.е. зависит от нагрузки машины. Принципиальная схема ДПВ изображена на рис., а схема двухфазной модели ЭМП двигателя последовательного возбуждения может быть получена аналогично схеме модели ЭМП ДНВ при включении обмотки возбуждения последовательно в цепь якоря (см. рис. ниже). При быстрых изменениях нагрузки, следовательно быстрых изменениях Ф, анализ динамических свойств двигателя без учета влияния вихревых токов, наводимых в сердечниках полюсов и станине, может привести к значительным ошибкам. Влияние этих токов может быть учтено добавлением к.з. обмотки на оси b, связанной с потоком Ф машины по этой оси коэффициентом связи, равным 1. С учетом этой фиктивной обмотки математическое описание процессов преобразования энергии в ДПВ имеет вид:
У двигателя последовательного возбуждения обмотка возбуждения включена последовательно с обмоткой якоря и его поток Ф является функцией тока якоря, т.е. зависит от нагрузки машины. Принципиальная схема ДПВ изображена на рис., а схема двухфазной модели ЭМП двигателя последовательного возбуждения может быть получена аналогично схеме модели ЭМП ДНВ при включении обмотки возбуждения последовательно в цепь якоря (см. рис. ниже). При быстрых изменениях нагрузки, следовательно быстрых изменениях Ф, анализ динамических свойств двигателя без учета влияния вихревых токов, наводимых в сердечниках полюсов и станине, может привести к значительным ошибкам. Влияние этих токов может быть учтено добавлением к.з. обмотки на оси b, связанной с потоком Ф машины по этой оси коэффициентом связи, равным 1. С учетом этой фиктивной обмотки математическое описание процессов преобразования энергии в ДПВ имеет вид:
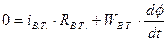

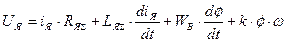
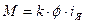 , где
, где 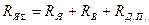
Индуктивность рассеяния якорной цепи LЯS ДНВ значительно меньше индуктивности LВ обмотки возбуждения, связанной с главным потоком двигателя, поэтому ею часто пренебрегают. Однако при этом нужно иметь в виду, что при LЯ=0 ток двигателя при изменении скачком приложенного напряжения тоже может измениться скачком.
Для практического использования написанными уравнениями в них необходимо исключить вихревой ток iВ.Т. и положить 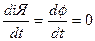 . Тогда
. Тогда
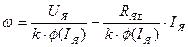 ;
; 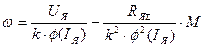
Дата добавления: 2015-10-05; просмотров: 1138;
