Эл.привода как динамической системы.

Механическая часть эл.привода представляет собой систему твердых тел, движущихся с различными скоростями. Уравнение движения ее можно определить на основе анализа запасов энергии в системе двигатель – рабочая машина, или на основе анализа второго закона Ньютона. Но наиблее общей формой записи диф. уравнений, определяющих движение системы, в которой число независимых переменных равно числу степеней свободы системы, является уравнение Лагранжа:

1) 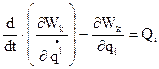, где

W_k – запас кинетической энергии; 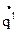– обобщенная скорость; q_i – обобщенная координата; Q_i – обобщенная сила, определенная суммой элементарных работ DA_i всех действующих сил на возможных перемещениях Dqi: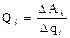

При наличии в системе потенциальных сил формула Лагранжа принимает вид:

2) 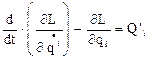, где

L=W_k-W_n функция Лагранжа, равная разности запасов кинетической W_k и потенциальной энергии W_n.

В качестве обобщенных координат, т.е. не зависимых переменных, могут быть приняты как различные угловые, так и линейные перемещения в системе. В трехмассовой упругой системе за обобщение координаты целесообразно принять угловое перемещение масс j₁,j₂,j₃ и соответствующие им угловые скорости w₁, w₂, w₃.

Запас кинетической энергии в системе: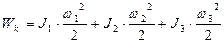

Запас потенциальной энергии деформации упругих элементов, подвергающихся скручиванию:

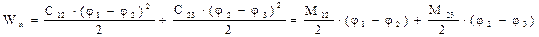
Здесь М₁₂ и М₂₃ – моменты упругого взаимодействия между инерционными массами J₁ и J₂, J₂ и J₃, зависящие от величины деформации j₁-j₂ и j₂-j₃.

На инерционную массу J₁ действуют моменты М и М_с1. Элементарная работа приложенных к J₁ моментов на возможном перемещении _Dj₁.

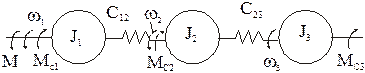
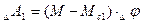Следовательно, обобщенная сила .

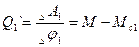Аналогично элементарная работа всех приложений ко 2-й и 3-й массам моментам на возможных перемещениях _Dj₂ и _Dj₃: 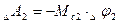, откуда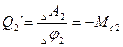

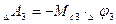, откуда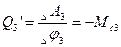

т.к. ко 2-й и 3-й массам электромагнитный момент двигателя не приложен. Функция Лагранжа L=W_k-W_n.

Учитывая значения Q1`,Q2`и Q3` и подставив их в уравнение Лагранжа, получим уравнения движения трехмассовой упругой системы

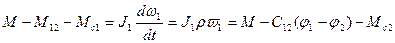
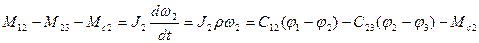
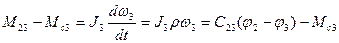
Здесь 1-е уравнение определяет движение инерционной массы J₁, 2-е и 3-е движение инерционных масс J₂ и J₃.

В случае двухмассовой системы Мс3=0; J3=0 уравнения движения имеют вид:

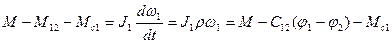
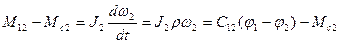
В случае жесткого приведенного механического звена ;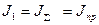

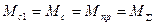
Уравнение движения имеет вид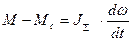

Это уравнение является основным уравнением движения эл.привода.

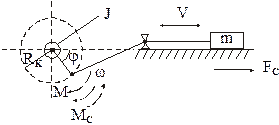В системе эл.привода некоторых механизмов содержится кривошипно – шатунные, кулисные, карданные передачи. Для таких механизмов радиус приведения “r” непостоянен, зависит от положения механизма, так для кривошипно шатунного механизма, изображенного на рис.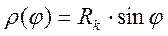

Получить уравнение движения в этом случае можно также на основе формулы Лагранжа или на основе составления энергетического баланса системы двигатель – рабочая машина. Воспользуемся последним условием.

Пусть J –суммарный приведенный к валу двигателя момент инерции всех жестко и линейно связанных вращающихся элементов, а m – суммарная масса элементов жестко и линейно связанных с рабочим органом механизма, движущаяся со скоростью V. Связь между w и V нелинейна, причем 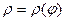. Запас кинетической энергии в системе:

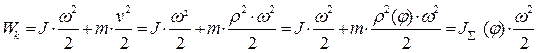
т.к. 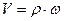, 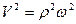и .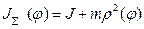

Здесь 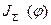- суммарный приведенный к валу двигателя момент инерции системы.

Динамическая мощность:

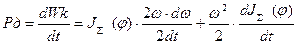
Динамический момент:

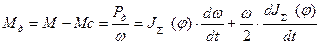, или т.к. 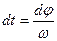, то

.

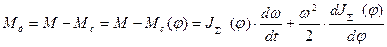Полученные уравнения движения позволяют анализировать возможные режимы движения эл.привода как динамической системы.

Возможны 2 режима (движения) электропривода: установившийся и переходный, причем установившийся режим может быть статическим или динамическим.

Установившийся статический режим эл.привода с жесткими связями имеет место в случае, когда 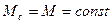, , 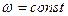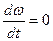. Для механизмов, у которых М_с зависит от угла поворота (например, кривошипно-шатунных), даже пр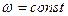и и 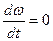статический режим отсутствует, а имеет место установившийся динамический режим.

Во всех остальных случаях, т.е. пр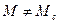и и 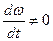имеет место переходный режим.

Переходным процессом эл.привода как динамической системы называют режим его работы при переходе от одного установившегося состояния к другому, когда изменяется ток, момент и скорость двигателя.

Переходные процессы всегда связаны с изменением скорости движения масс электропривода, поэтому всегда являются динамическими процессами.

Без переходного режима не совершается работа ни одного эл.привода. Эл.привод работает в переходных режимах при пуске, торможении, изменении скорости, реверсе, свободном выбеге (отключение от сети и движении по инерции).

Причинами возникновения переходных режимов являются или воздействия на двигатель с целью управления им изменением подводимого напряжения или его частоты, изменением сопротивления в цепях двигателя, изменение нагрузки на валу, изменение момента инерции.

Переходные режимы (процессы) возникают также в результате аварии или др. случайных причин, например, при изменении величины напряжения или его частоты, обрыве фаз, возникновении не симметрии питающего напряжения и т.п. Внешняя причина (возмущающее воздействие) является только внешним толчком, побуждающим эл.привод к переходным процессам.