Вода — растворитель
Вода хорошо растворяет полярные, или гидрофильные вещества — например, растворимые соли, белки, сахара. Молекулы воды окружают ионы или молекулы вещества, отделяя тем самым частицы друг от друга. Следовательно, в растворе молекулы (или ионы) смогут двигаться более свободно, значит, быстрее вступить в химическую реакцию. Гидрофобные вещества не будут растворяться в воде, зато молекулы H2O смогут отделить гидрофобное вещество от самой толщи воды. Например, жиры - фосфолипиды, из которых состоит клеточная мембрана, могут благодаря взаимодействию с водой формировать липидный бислой.
UNIT 30 Diffusion
Although diffusion is clearly caused by the motion of particles through space, for our biological purposes here it can be regarded as the mixing of particles amongst one another. The phenomenon was investigated first by the English botanist Robert Brown, who in 1828 observed pollen particles in a glass of water, with the help of a microscope, and noticed their irregular and apparently erratic movements. These movements are now known as Brownian motion.
In 1905, the year when he also produced his epoch-making papers on special relativity and the photoelectric effect, Albert Einstein published a quantitative explanation of this motion. He showed that it is caused by the impacts, on the pollen particles, of the even smaller (and thus sub-microscopic) water molecules. In the Einstein analysis, the water molecules would be more mobile than the pollen particles, because of their smaller size, and this is why it is valid to think in terms of the pollen particles being hit by them, and not the reverse. The analysis is not limited to such situations of size disparity; it is equally applicable when the various types of particle have roughly the same size. Moreover, there is not a restriction to the liquid domain first studied by Brown. The Einstein principles are just as valid for gases and solids (though there are some additional correlation factors in the case of the latter - we need not go into them here).
If we regard the movements of a specific particle, we discover that we can divide its trajectory into small straight paths; the particle appears to jump from point to point, in an essentially ballistic manner. If each jump is independent of the particle's prior history, the movement process is said to be stochastic, and the movements themselves are said to describe a random walk. (The totality of the stochastic movements is known as a Markov chain – In honour of Andrei Markov.) The classic result pertaining to the random walk (for steps of unit length), in the absence of any directional bias, is that the mean distance, r, travelled in any number of steps, m, equals zero, whereas the root mean squared distance, rrms equals 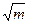 .
.
Дата добавления: 2015-09-29; просмотров: 613;
