Кейс 1 подзадача 3
1. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 4 % с вероятностью 0,9 или подешеветь на 4 % с вероятностью 0,1. Предполагается, что еженедельные изменения цен независимы. Прошло две недели.
Математическое ожидание курсовой стоимости ценой бумаги будет равно …
1065,024
1065,00
1064,976
1000,00
Решение:
Составим закон распределения вероятностей дискретной случайной величины 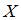 – курсовой стоимости ценной бумаги, как
– курсовой стоимости ценной бумаги, как
где 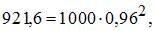 а
а 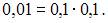
Тогда 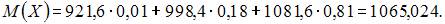
2. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 6 % с вероятностью 0,75 или подешеветь на 6 % с вероятностью 0,25. Предполагается, что еженедельные изменения цен независимы. Прошло две недели.
Математическое ожидание курсовой стоимости ценой бумаги будет равно …
1060,90
1060,00
1059,10
1000,00
Решение:
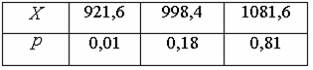
Составим закон распределения вероятностей дискретной случайной величины 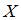 – курсовой стоимости ценной бумаги, как:
– курсовой стоимости ценной бумаги, как:
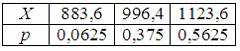
где 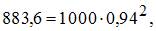 а
а 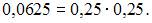
Тогда 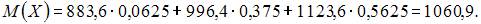
3. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 5 % с вероятностью 0,8 или подешеветь на 5 % с вероятностью 0,2. Предполагается, что еженедельные изменения цен независимы. Прошло две недели.
Математическое ожидание курсовой стоимости ценой бумаги будет равно …
1060,90
1050,00
1059,10
1000,00
Решение:
Составим закон распределения вероятностей дискретной случайной величины 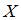 – курсовой стоимости ценной бумаги, как
– курсовой стоимости ценной бумаги, как
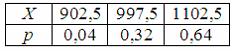
где 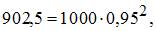 а
а 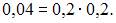
Тогда 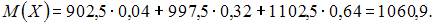
4. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 2 % с вероятностью 0,6 или подешеветь на 2 % с вероятностью 0,4. Предполагается, что еженедельные изменения цен независимы. Прошло две недели.
Математическое ожидание курсовой стоимости ценой бумаги будет равно …
1008,016
1008,00
1007,944
1000,00
Решение:
Составим закон распределения вероятностей дискретной случайной величины 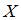 – курсовой стоимости ценной бумаги, как
– курсовой стоимости ценной бумаги, как
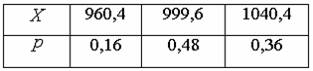
где 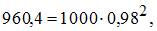 а
а 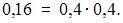
Тогда 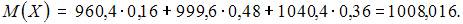
Дата добавления: 2015-09-29; просмотров: 8792;
