Местные гидравлические сопротивления
Все гидравлические потери энергии делятся на два типа: потери на трение по длине трубопроводов и местные потери, вызванные такими элементами трубопроводов, в которых вследствие изменения размеров или конфигурации русла происходит изменение скорости потока, отрыв потока от стенок русла и возникновение вихреобразования.
Простейшие местные гидравлические сопротивления можно разделить на расширения, сужения и повороты русла, каждое из которых может быть внезапным или постепенным. Более сложные случаи местного сопротивления представляют собой соединения или комбинации перечисленных простейших сопротивлений.
|
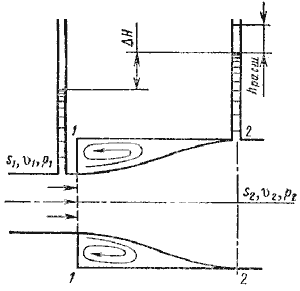
1. Внезапное расширение русла. Потеря напора (энергии) при внезапном расширении русла расходуется на вихреобразование, связанное с отрывом потока от стенок, т.е. на поддержание вращательного непрерывного движения жидких масс с постоянным их обновлением (рис. 10).
Рис. 10. Внезапное расширение трубы
При внезапном расширении русла (трубы) (рис.10) поток срывается с угла и расширяется не внезапно, как русло, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии. Рассмотрим два сечения потока: 1-1 - в плоскости расширения трубы и 2-2 - в том месте, где поток, расширившись, заполнил все сечение широкой трубы. Так как поток между рассматриваемыми сечениями расширяется, то скорость его уменьшается, а давление возрастает. Поэтому второй пьезометр показывает высоту на ΔHбольшую, чем первый; но если бы потерь напора в данном месте не было, то второй пьезометр показал бы высоту большую еще на hрасш. Эта высота и есть местная потеря напора на расширение, которая определяется по формуле: 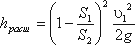 (11)
(11)
где S1, S2- площадь поперечных сечений 1-1 и 2-2.
Это выражение является следствием теоремы Борда: потеря напора при внезапном расширении русла равна скоростному напору, определённому по разности скоростей: 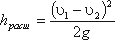 Выражение (1 - S1/S2)2 обозначается греческой буквой ζ(дзета) и называется коэффициентом потерь, таким образом:
Выражение (1 - S1/S2)2 обозначается греческой буквой ζ(дзета) и называется коэффициентом потерь, таким образом: 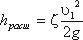 (12)
(12)
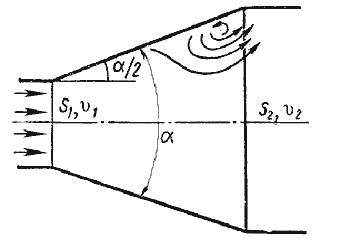
2. Постепенное расширение русла. Постепенно расширяющаяся труба называется диффузором (рис. 11). Течение скорости в диффузоре сопровождается её уменьшением и увеличением давления, а, следовательно, преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.
|
Рис. 11. Постепенное расширение трубы (диффузор)
Кроме того, в диффузоре имеются и обычные потери на трение, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых: 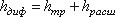 (13)
(13)
где hтр и hрасш- потери напора на трение и расширение (вихреобразование).
3. Внезапное сужение русла. В этом случае потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока (рис. 12).
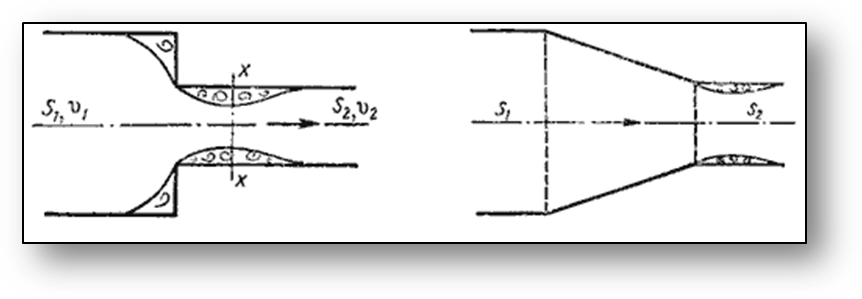
| Рис. .12. Внезапное сужение трубы | Рис. 13. Конфузор |
Полная потеря напора определится по формуле: 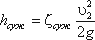
где коэффициент сопротивления сужения определяется по полуэмпирической формуле И.Е. Идельчика: 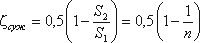 , в которой n = S1/S2 - степень сужения.
, в которой n = S1/S2 - степень сужения.
При выходе трубы из резервуара больших размеров, когда можно считать, что S2/S1 = 0, а также при отсутствии закругления входного угла, коэффициент сопротивления ζсуж = 0,5.
4. Постепенное сужение русла. Данное местное сопротивление представляет собой коническую сходящуюся трубу, которая называется конфузором (рис. 13). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. В конфузоре имеются лишь потери на трение.
Небольшое вихреобразование и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилиндрической. Закруглением входного угла можно значительно уменьшить потерю напора при входе в трубу. Конфузор с плавно сопряженными цилиндрическими и коническими частями называется соплом (рис. 14).
|
Рис. 14. Сопло
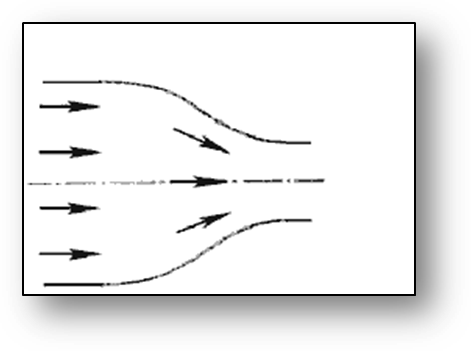
5. Внезапный поворот трубы (колено). Данный вид местного сопротивления (рис. 15) вызывает значительные потери энергии, т.к. в нем происходят отрыв потока и вихреобразования, причем потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле:
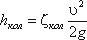
где ζкол - коэффициент сопротивления колена круглого сечения, который определяется по графику в зависимости от угла колена δ (рис. 16).
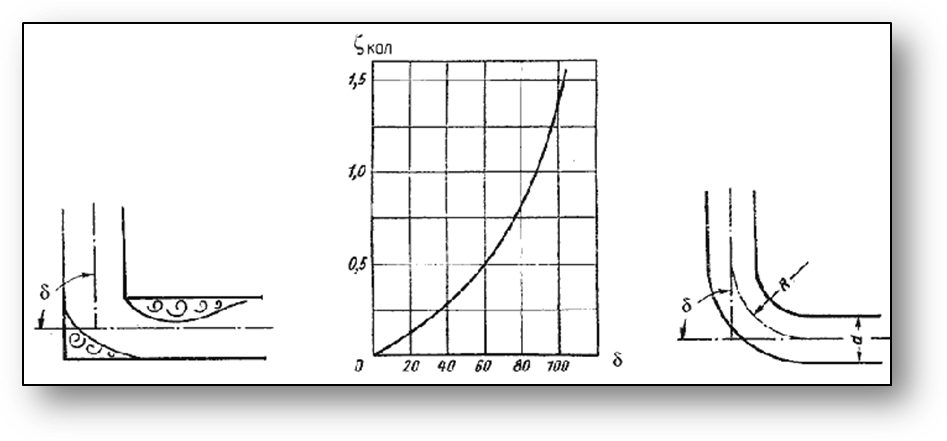
| Рис. 15. Колено | Рис. 16. Зависимости ζкол от угла δ | Рис. 17. Отвод |
6. Постепенный поворот трубы (закругленное колено или отвод). Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R / d (рис. 17). Коэффициент сопротивления отвода ζотвзависит от отношения R / d, угла δ, а также формы поперечного сечения трубы.
Потеря напора в колене определится как 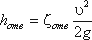
Все выше изложенное относится к турбулентному движению жидкости. При ламинарном движении местные сопротивления играют малую роль при определении общего сопротивления трубопровода. Кроме этого закон сопротивления при ламинарном режиме является более сложным и исследован в меньшей степени.
[1] Ж.Пуазейль (1799-1869) – французский учёный, получивший формулу экспериментальным путём в 1840 г.
[2] Этого механика часто сгоряча называют грузинским академиком Иваном Никурадзе. Но в Грузии он не работал, да и к академиям отношения не имел. О его работах известно очень много, а о нем самом - очень мало. Все разгадки - ниже.
Вано Ильич Никурадзе (1894-1979) родился в Самтредиа, учился в Кутаиси, затем поступил вместе с братом в Тбилисский университет. При содействии декана Петре Меликишвили он в 1919 г. был включен в группу студентов, направленную для обучения за границу. И. Никурадзе учился в Геттингенском университете и в 1923 г. защитил под руководством Людвига Прандтля диссертацию «Наблюдения за распределением скорости в турбулентном течении».
В 1921 г. в Грузии установилась советская власть, и Никурадзе получил в консульстве советский паспорт. С 1926 г. начались гонения на ученых, работающих за рубежом, и Никурадзе пришлось остаться в Германии. Также в Германии остался и его брат Александр (он же A. Sanders), ставший специалистом по физике твердого тела, этнографии и истории.
После защиты Иоганн Никурадзе работал в Институте гидроаэродинамики Кайзера Вильгельма в Гёттингене, директором которого (1925-47 гг.) был Л. Прандтль. Он изучал трение при турбулентном течении в шероховатых трубах и вывел эмпирическую формулу для коэффициента сопротивления (формула Прандтля-Никурадзе). Шероховатость в латунных трубах создавалась наклеиванием песчинок известного размера. Оказалось, что при малых числах Рейнольдса, когда шероховатости лежат внутри ламинарного пограничного слоя, сопротивление не зависит от размера шероховатости и совпадает с сопротивлением в гладкой трубе. Далее Никурадзе выделил еще три диапазона чисел Рейнольдса и получил для них разные эмпирические зависимости коэффициента сопротивления. На основе его работ затем исследовалось сопротивление в трубах с «естественной» шероховатостью (настолько, насколько естественны сами трубы).
Никурадзе стал профессором в университете Бреслау (1934 - 1945). С 1945 года он почетный профессор Технического университета в Аахене.
Дата добавления: 2015-09-29; просмотров: 1819;
