Исходные данные.
| № варианта | Ширина русла В, м | Расход воды Q,м3/с | Максимальная глубина Нmax, м | Шероховатость русла, n | Ширина фронта сброса воды В0,м | Температура сбрасываемой воды tв, °С | Скорость ветра, м/с | Температура воздуха, °С | Влажность воздуха, гПа | Облачность в долях единицы | ||||
| w2 | w’2 | q2 | q’2 | е2 | е’2 | N | N’ | |||||||
| 0,015 | 4,0 | -0,5 | -15 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -1,0 | -16 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -1,5 | -17 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -2,0 | -18 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -2,5 | -19 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -3,0 | -20 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -3,5 | -21 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -4,0 | -22 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -4,5 | -23 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -5,0 | -24 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -0,5 | -25 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -1,0 | -26 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -1,5 | -27 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -2,0 | -28 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -2,5 | -29 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -3,0 | -30 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -3,5 | -31 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -4,0 | -32 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -4,5 | -33 | 3,1 | 0,9 | 0,7 | 0,2 | |||||||
| 0,015 | 4,0 | -5,0 | -34 | 3,1 | 0,9 | 0,7 | 0,2 |
Примечание. 1. Сбросное отверстие шириной В0 расположено у одного из берегов. 2. Значения метеовеличин приведены на начало (w2, q2, е2, N) и конец (w’2, q’2, е’2, N’) волны холода. 3. Облачность в начале волны холода низкая, в конце высокая. 4. Студент-заочник выбирает тот номер варианта, который совпадает с последней цифрой номера го зачетной книжки (или двумя последними).
Изучая специальную литературу по данной теме, студент должен разобраться в структуре эмпирических формул типа (1), составить таблицу значений параметров j, n, указав фамилии исследователей и названия объектов, для которых эти значения параметров вычислены.
Студент может сделать попытку установить значение параметров j и n в формуле (1) для исследуемого им водного объекта. При наличии достаточно большого количества данных синхронных наблюдений над толщиной ледяного покрова и температурой воздуха студент может попытаться получить собственную формулу вида (1). Для этого нужно прологарифмировать значения толщины льда (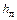 
), взятые по нарастающей, и соответствующие им суммы температур воздуха 
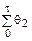. Затем, на миллиметровой бумаге, выбрав соответствующие масштабы, построить систему координат: ln 
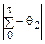– ось абсцисс; ln 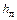– ось ординат. В этой системе нанести точки, соответствующие каждой паре значений ln 
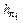и ln 
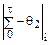. Затем по совокупности всех точек провести осредненную прямую, которая описывается уравнением вида
ln 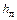= lnj + n ln 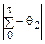. (2)
Если прямую на графике продолжить до пересечения с осью ординат, то она пересечет последнюю в точке ln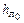 
= lnj. Величина n равна тангенсу угла наклона a построенной прямой, который можно легко определить, взяв две точки на прямой. Если первая из этих точек имеет координаты 
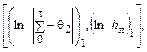а вторая 
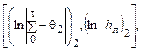то
n = tg a = 
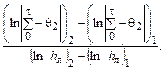(3)
После этого нужно только по величине lnj определить значение j. При определении параметров формулы j и n толщину льда удобнее выражать в см.
Полученные по различным формулам расчетные данные о нарастании ледяного покрова должны быть сопоставлены между собой, а также с данными наблюдений. Для большей наглядности ход изменения количественных характеристик явлений во времени и результаты сопоставления величин следует иллюстрировать соответствующими графиками и таблицами.
В заключении студент должен сделать конкретные выводы, к которым он пришел в результате выполнения работы, и, по возможности, привести свои соображения о задачах и путях дальнейших исследований зимнего термического и ледового режимов данного объекта.
Дата добавления: 2015-09-29; просмотров: 741;