Исходные данные. Номер измерения l, м v, см v2, см2 68,31 –1 68,30 –2

Номер измерения	l, м	v, см	v2, см2
	68,31	–1
	68,30	–2
	68,34	+2
	68,32
	68,33	+1

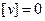
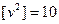
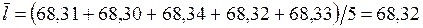м;

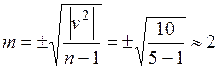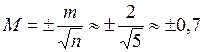см;

см;

.

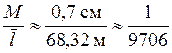Пример 3.В треугольнике на плане измерены основание м с 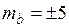см и высота 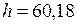м с 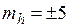см. Определить относительную среднюю квадратическую погрешность площади треугольника .

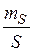Площадь треугольника участка

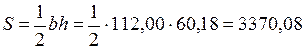м².

Найдем частные производные от функции S по аргументам b и h:

; .

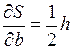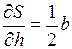Тогда

м².

.

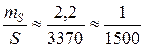Следует отметить, что рассмотренные выше примеры относятся к равноточным измерениям. Случай неравноточных измерений в данной работе не рассматривается.

[1] В прямоугольной системе значение координат принято выражать в метрах. При проведении измерений в данном случае допускается выражать координаты в километрах.