УРАВНЕНИЕ НЕРАЗРЫВНОСТИ ДЛЯ ПОТОКА

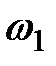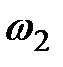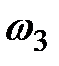В потоке конечных размеров (рис. 3.6) выделим сечения 1-1, 2-2 и 3-3, расположенные на некотором расстоянии друг от друга. Площади живых сечений потока будут , и . Живые сечения элементарной струйки, выделенной в потоке, соответственно равны 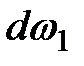, 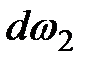и .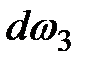

Скорости струйки в сечениях - , , .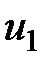

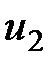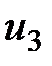Согласно уравнению неразрывности для струйки жидкости

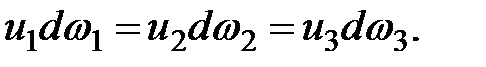(3.23)

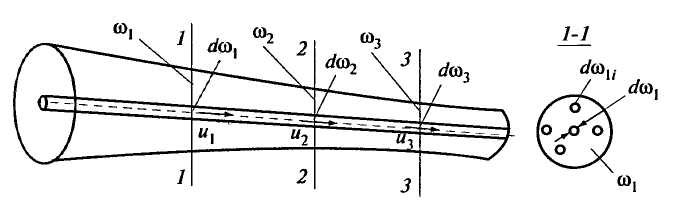
Рис. 3.6. К выводу уравнения неразрывности потока

Согласно струйчатой модели поток состоит из элементарных струек, поэтому, интегрируя по каждому из живых сечений 1-1, 2-2 и 3-3 уравнение (3.23), получаем

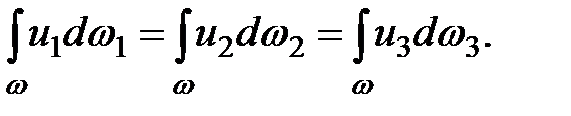(3.24)

Интеграл 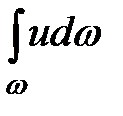- расход 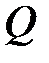, проходящий через живое сечение. Через среднюю скорость расход .

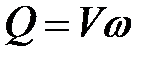Таким образом, можно записать:

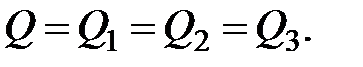
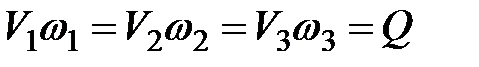(3.25)

Уравнение (3.25) для потока конечных размеров при установившемся движении жидкости является уравнением неразрывности.

Для разных сечений потока согласно (3.25) получим соотношение скоростей в живых сечениях:

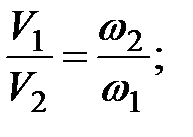
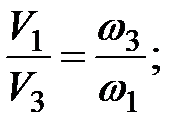
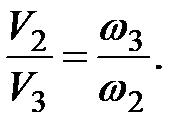(3.26)