Перевод числа из системы с основанием p в систему с основанием q.

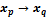(метод деления).

Пример 1. Перевод числа из системы с основанием 10 в систему с основанием 2.

Возьмём десятичное число 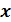= 121 и поделим его на основание двоичной системы, то есть число 2. Деление будем производить уголком:

;

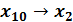Результат собирается из остатков в обратном порядке, начиная с последнего частного:

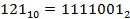
Пример 2.Перевод числа из системы с основанием 10 в систему с основанием 3.

Возьмём десятичное число 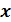= 121 и поделим его на основание троичной системы, то есть число 3. Деление будем производить уголком:

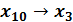
Результат собирается из остатков в обратном порядке, начиная с последнего частного:

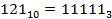
Пример 3.Перевод числа из системы с основанием 10 в систему с основанием 8.

Возьмём десятичное число 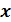= 121 и поделим его на основание восьмеричной системы, то есть число 8. Деление будем производить уголком:

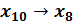
Результат собирается из остатков в обратном порядке, начиная с последнего частного: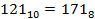

Теперь число 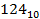переведём в восьмеричную систему счисления. Для этого число 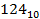будем делить на число 8:

Как мы видим, остаток от первого деления равен 4. То есть младший разряд восьмеричного числа содержит цифру 4. Остаток от второго деления равен 7. то есть второй разряд восьмеричного числа – это цифра 7. Старший разряд получился равным 1. То есть в результате многократного деления мы получили восьмеричное число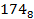

Пример 4.Перевод числа из системы с основанием 10 в систему с основанием 16.

Возьмём десятичное число 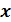= 124 и поделим его на основание шестнадцатеричной системы, то есть число 16:

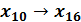
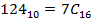
Последний остаток равен 12, в шестнадцатеричной системе это число C₁₆