Карты входов

При анализе карт входов рекомендуют использовать сразу несколько карт. Исследуем фрагмент карты, состоящий из карт трех входов, который приведен на рисунке 10.18.

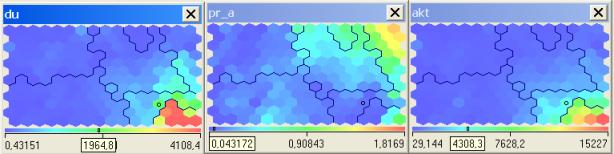
Рисунок 10.18 - Карты трех входов

На одной из карт выделяем область с наибольшими значениями показателя. Далее имеет смысл изучить эти же нейроны на других картах.

На первой карте наибольшие значения имеют объекты, расположенные в правом нижнем углу. Рассматривая одновременно три карты, мы можем сказать, что эти же объекты имеют наибольшие значения показателя, изображенного на третьей карте. Также по раскраске первой и третьей карты можно сделать вывод, что существует взаимосвязь между этими показателями.

Также мы можем определить, например, такую характеристику: кластер, расположенный в правом верхнем углу, характеризуется низкими значениями показателей du (депозиты юридических лиц) и akt (активы банка) и высокими значениями показателей pr_a (прибыльность активов).

Эта информация позволяет так охарактеризовать кластер, находящийся в правом верхнем углу: это банки с небольшими активами, небольшими привлеченными депозитными средствами от юридических лиц, но с наиболее прибыльными активами, т.е. это группа небольших, но наиболее прибыльных банков.

Это лишь фрагмент вывода, который можно сделать, исследуя карту.

На следующем рисунке (рисунок 10.19) приведена иллюстрация карт входов и выходов, последняя - эта карта кластеров. Здесь мы видим несколько карт входов (показателей деятельности банков) и сформированные кластеры, каждый из которых выделен отдельным цветом.

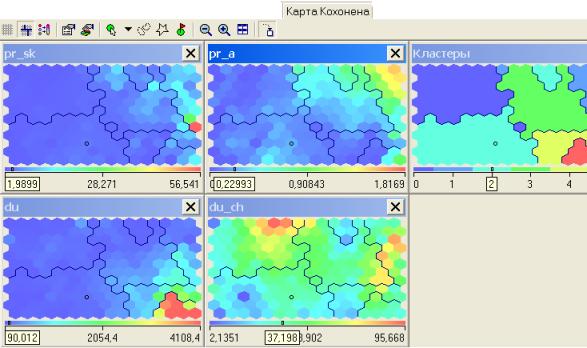
Рисунок 10.19 - Карты входов и выходов

Для нахождения конкретного объекта на карте необходимо нажать правой кнопкой мыши на исследуемом объекте и выбрать пункт "Найти ячейку на карте". Выполнение этой процедуры показано на рисунке 10.20. В результате мы можем видеть как сам объект, так и значение того измерения, которое мы просматриваем. Таким образом, мы можем оценить положение анализируемого объекта, а также сравнить его с другими объектами.

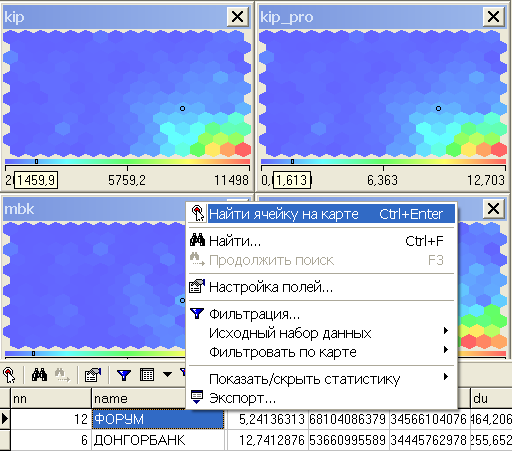
Рисунок 10.20 - Ячейка на карте

В результате применения самоорганизующихся карт многомерное пространство входных факторов было представлено в двухмерном виде, в котором его достаточно удобно анализировать.

Банки были классифицированы на 7 групп, для каждой из которых возможно определение конкретных характеристик, исходя из раскраски соответствующих показателей.

Выводы

Основное отличие этих сетей от других моделей состоит в наглядности и удобстве использования. Эти сети позволяют упростить многомерную структуру, их можно считать одним из методов проецирования многомерного пространства в пространство с более низкой размерностью. Интенсивность цвета в определенной точке карты определяется данными, которые туда попали: ячейки с минимальными значениями изображаются темно-синим цветом, ячейки с максимальными значениями - красным.

Другое принципиальное отличие карт Кохонена от других моделей нейронных сетей - иной подход к обучению, а именно - неуправляемое или неконтролируемое обучение. Этот тип обучения позволяет данным обучающей выборки содержать значения только входных переменных. Сеть Кохонена учится понимать саму структуру данных и решает задачи кластеризации

11 МЕТОДЫ КЛАСТЕРНОГО АНАЛИЗА

В лекции рассматриваются основы кластерного анализа, математические характеристики кластера. Описаны две группы иерархического кластерного анализа: агломеративные и дивизимные методы.

В этой лекции мы опишем понятие "кластер" с математической точки зрения, а также рассмотрим методы решения задач кластеризации - методы кластерного анализа.

Термин кластерный анализ, впервые введенный Трионом (Tryon) в 1939 году, включает в себя более 100 различных алгоритмов.

В отличие от задач классификации, кластерный анализ не требует априорных предположений о наборе данных, не накладывает ограничения на представление исследуемых объектов, позволяет анализировать показатели различных типов данных (интервальным данным, частотам, бинарным данным). При этом необходимо помнить, что переменные должны измеряться в сравнимых шкалах.

Кластерный анализ позволяет сокращать размерность данных, делать ее наглядной.

Кластерный анализ может применяться к совокупностям временных рядов, здесь могут выделяться периоды схожести некоторых показателей и определяться группы временных рядов со схожей динамикой.

Кластерный анализ параллельно развивался в нескольких направлениях, таких как биология, психология, др., поэтому у большинства методов существует по два и более названий. Это существенно затрудняет работу при использовании кластерного анализа.

Задачи кластерного анализа можно объединить в следующие группы:

1. Разработка типологии или классификации.

2. Исследование полезных концептуальных схем группирования объектов.

3. Представление гипотез на основе исследования данных.

4. Проверка гипотез или исследований для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных.

Как правило, при практическом использовании кластерного анализа одновременно решается несколько из указанных задач.

Рассмотрим пример процедуры кластерного анализа.

Допустим, мы имеем набор данных А, состоящий из 14-ти примеров, у которых имеется по два признака X и Y. Данные по ним приведены в таблице 11.1.

Таблица 11.1. Набор данных А

Данные в табличной форме не носят информативный характер. Представим переменные X и Y в виде диаграммы рассеивания, изображенной на рисунке 11.1.

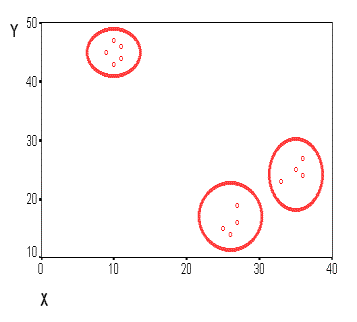
Рисунок 11.1 - Диаграмма рассеивания переменных X и Y

На рисунке мы видим несколько групп "похожих" примеров. Примеры (объекты), которые по значениям X и Y "похожи" друг на друга, принадлежат к одной группе (кластеру); объекты из разных кластеров не похожи друг на друга.

Критерием для определения схожести и различия кластеров является расстояние между точками на диаграмме рассеивания. Это сходство можно "измерить", оно равно расстоянию между точками на графике. Способов определения меры расстояния между кластерами, называемой еще мерой близости, существует несколько. Наиболее распространенный способ - вычисление евклидова расстояния между двумя точками i и j на плоскости, когда известны их координаты X и Y:

(11.1)

Примечание: чтобы узнать расстояние между двумя точками, надо взять разницу их координат по каждой оси, возвести ее в квадрат, сложить полученные значения для всех осей и извлечь квадратный корень из суммы.

Когда осей больше, чем две, расстояние рассчитывается таким образом: сумма квадратов разницы координат состоит из стольких слагаемых, сколько осей (измерений) присутствует в нашем пространстве. Например, если нам нужно найти расстояние между двумя точками в пространстве трех измерений (такая ситуация представлена на рисунке 11.2), формула (11.1) приобретает вид:

(11.2)

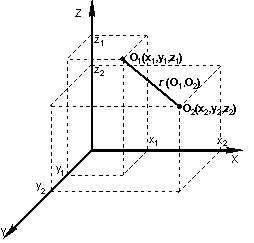
Рисунок 11.2 - Расстояние между двумя точками в пространстве трех измерений

Кластер имеет следующие математические характеристики: центр, радиус, среднеквадратическое отклонение, размер кластера.

Центр кластера - это среднее геометрическое место точек в пространстве переменных.

Радиус кластера - максимальное расстояние точек от центра кластера.

Как было отмечено в одной из предыдущих лекций, кластеры могут быть перекрывающимися. Такая ситуация возникает, когда обнаруживается перекрытие кластеров. В этом случае невозможно при помощи математических процедур однозначно отнести объект к одному из двух кластеров. Такие объекты называют спорными.

Спорный объект - это объект, который по мере сходства может быть отнесен к нескольким кластерам.

Размер кластера может быть определен либо по радиусу кластера, либо по среднеквадратичному отклонению объектов для этого кластера. Объект относится к кластеру, если расстояние от объекта до центра кластера меньше радиуса кластера. Если это условие выполняется для двух и более кластеров, объект является спорным.

Работа кластерного анализа опирается на два предположения. Первое предположение - рассматриваемые признаки объекта в принципе допускают желательное разбиение пула (совокупности) объектов на кластеры. В начале лекции мы уже упоминали о сравнимости шкал, это и есть второе предположение - правильность выбора масштаба или единиц измерения признаков.

Выбор масштаба в кластерном анализе имеет большое значение. Рассмотрим пример. Представим себе, что данные признака х в наборе данных А на два порядка больше данных признака у: значения переменной х находятся в диапазоне от 100 до 700, а значения переменной у - в диапазоне от 0 до 1.

Тогда, при расчете величины расстояния между точками, отражающими положение объектов в пространстве их свойств, переменная, имеющая большие значения, т.е. переменная х, будет практически полностью доминировать над переменной с малыми значениями, т.е. переменной у. Таким образом из-за неоднородности единиц измерения признаков становится невозможно корректно рассчитать расстояния между точками.

Эта проблема решается при помощи предварительной стандартизации переменных. Стандартизация (standardization) или нормирование (normalization) приводит значения всех преобразованных переменных к единому диапазону значений путем выражения через отношение этих значений к некой величине, отражающей определенные свойства конкретного признака. Существуют различные способы нормирования исходных данных.

Два наиболее распространенных способа:

· деление исходных данных на среднеквадратичное отклонение соответствующих переменных;

· вычисление Z-вклада или стандартизованного вклада.

Наряду со стандартизацией переменных, существует вариант придания каждой из них определенного коэффициента важности, или веса, который бы отражал значимость соответствующей переменной. В качестве весов могут выступать экспертные оценки, полученные в ходе опроса экспертов - специалистов предметной области. Полученные произведения нормированных переменных на соответствующие веса позволяют получать расстояния между точками в многомерном пространстве с учетом неодинакового веса переменных.

В ходе экспериментов возможно сравнение результатов, полученных с учетом экспертных оценок и без них, и выбор лучшего из них.