Условные вероятности и независимость событий. Формула полной вероятности

1. Понятие условной вероятности.При анализе различных явлений часто возникает вопрос следующего рода: как влияет на возможность осуществления некоторого события B наступление некоторого другого события A? В некоторых случаях ответ очевиден, например, если A и B несовместные события, т. е. то наступление события A исключает возможность наступления события B. В общем же случае ответ на этот вопрос даётся в терминах понятия условной вероятности. Чтобы подойти к определению этого нового понятия, рассмотрим следующий пример.

Изурны, содержащей 7 белых и 3 чёрных шара, по схеме выбора без возвращения последовательно извлекаются два шара. Пусть событие A означает, что первый шар – белый, а B – второй шар тоже белый. Наконец, введём событие С = A B = {оба шара белые}. Вычислим вероятности этих событий.

При вычислении вероятности события С воспользуемся классическим определением вероятности. В рассматриваемом случае общее число исходов эксперимента 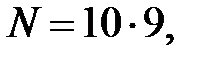а число благоприятных (для события С) исходов 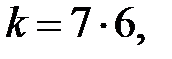поэтому по формуле (1.6)[1]

Ясно, что 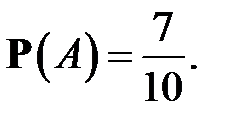Вероятность же события B зависит от того, какой шар выбран первым. Если наступило событие 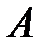, то в урне осталось 6 белых и 3 чёрных шара, поэтому вероятность вынуть белый шар во второй раз равна 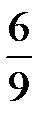; эта вероятность обозначается и называется условной вероятностью события B при условии, что 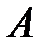наступило. Мы видим, что

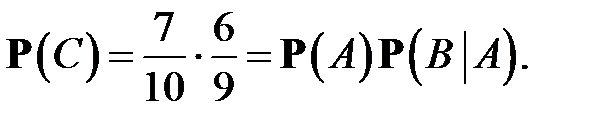
Но в то же время С = A B, поэтому предыдущее равенство можно записать в виде

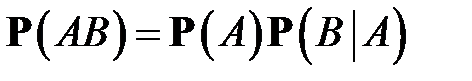(1 )

или

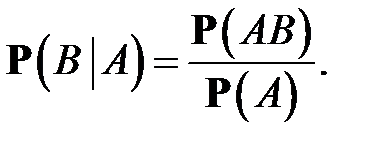(2)

Равенство (2) положено в основу общего определения условной вероятности (здесь, конечно, должно выполняться условие ). Формула же (1) определяет правило умножения вероятностей.Оно формулируется так:

вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло.

Это правило допускает обобщение и на большее число событий. Например, для трёх событи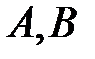й и оно имеет вид:

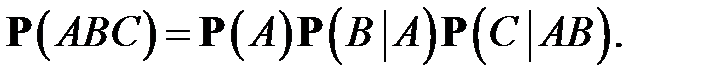
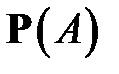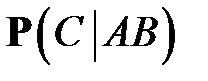Здесь называют безусловной вероятностью, а и – условными вероятностями.

Пример 1.На некотором предприятии изделий признаются пригодными (пригодность конкретного изделия – это событие A); из каждой сотни годных изделий в среднем 75 оказываются первого сорта (то, что изделие первого сорта – это событие B). Найти вероятность того, что случайно взятое изделие окажется первого сорта (оно должно быть одновременно и пригодным, и первого сорта).

В силу условия задачи

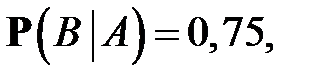
поэтому по правилу умножения (1)

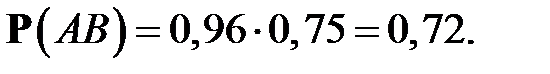
Пример 2.Ребёнок,играя десятью кубиками с буквами М, М, Т, Т, А, А, А, К, И, Е, сложил слово «МАТЕМАТИКА». Какова вероятность такого события (обозначим его ), если считать, что ребёнок неграмотный и складывает кубики в случайном порядке?

Р е ш е н и е. Введём события М, Т, А, К, И, Е, обозначающие выбор соответствующей буквы. Тогда по правилу умножения и по классическому определению вероятности имеем:

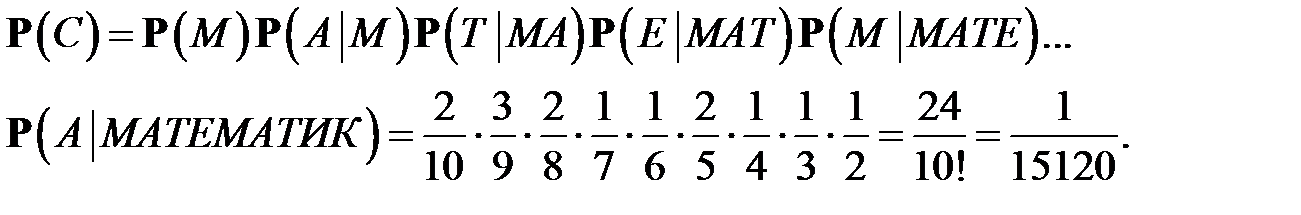
Эта вероятность ничтожно мала, поэтому событие практически невозможно! Если же оно осуществилось, то следует считать гипотезу о неграмотности ребёнка неверной. Детальнее вопросы проверки различных статистических гипотез будут обсуждаться позднее.

Пример 3.Приведём ещё одно решение задачи о ключах(см. пример 1.7). По правилу умножения и по классическому определению вероятности можем записать следующую цепочку равенств:

Естественно, результат получился тот же.

2. Независимость событий.С условной вероятностью связано одно из важнейших понятий ТВ – понятие независимости случайных событий. Естественно считать, что событие B не зависит от события A, если наступление события A никак не влияет на вероятность осуществления события B, т. е. условная вероятность события B при условии, что 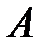наступило, равна безусловной вероятности события B:

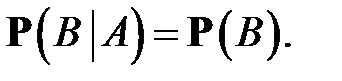(3)

Если имеет место (3), то из (1) следует равенство

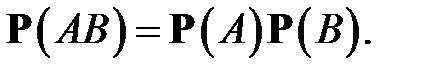(4)

Это равенство симметрично относительно событий A и B, поэтому, если B не зависит от A, то и A не зависит от B, т. е. независимость двух событий есть свойство взаимное. Равенство (4) и принимается за определение независимости событий A и B.

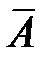Смысл определения независимости заключается в том, что если произошло одно из независимых событий, то это никак не влияет на вероятность осуществления другого события. При этом, если A и B независимы, то также независимы A и , и B, и .

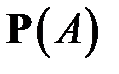Обычно независимость событий ясна из физической сущности анализируемого явления. Например, при повторных бросаниях монеты выпадение герба и решётки в разных бросаниях будут независимыми событиями. С помощью равенства (4) обычно вычисляют вероятность одновременного осуществления независимых событий A и B, зная вероятности и .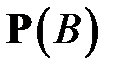

Пример 4.Два стрелка делают по одному выстрелу, каждый по своей мишени. Вероятность поражения цели 1-м стрелком (событие ) равна 0,7, а вторым (событие ) – 0,9. Найти вероятности следующих событий: A={обе цели поражены}, B={ни одна из целей не поражена}, С ={поражена только одна цель}.

Р е ш е н и е. Естественно считать, что в данном случаесобытия и независимы. Поэтому, так как 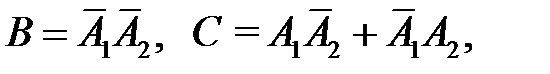то

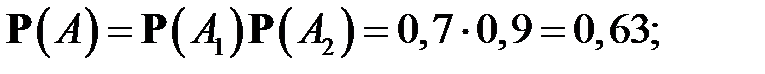
Обратим внимание на то, что события A, B и С образуют полную систему, так как они попарно несовместны и сумма их вероятностей равна единице.

Пример 5.Из колоды в 36 карт наугад вынимается карта. Рассмотрим события A={вынута «пика»} и B={ вынута «дама»}. Будут ли эти события независимыми? Здесь событие AB означает, что вынута «дама пик». По классическому определению вероятности имеем:

следовательно, выполняется равенство (4), и потому события независимы.

Понятие независимости распространяется на случай нескольких событий. События 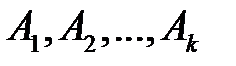называются взаимно независимыми (или независимыми в совокупности, или просто независимыми), если для всех комбинаций индексов выполняются равенства

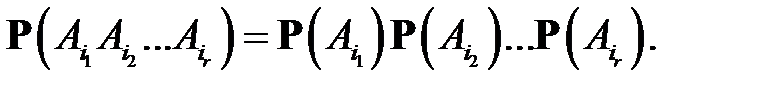
Если эти равенства выполняются только при r = 2, то события называют попарно независимыми. Отметим, что из попарной независимости не следует независимость в совокупности, как показывает следующий пример.

Пример 6.На плоскость бросается тетраэдр, грани которого окрашены так: три грани – одним цветом, соответственно, красным (К), белым (Б) и чёрным (Ч), а четвёртая – всеми тремя. Исходом опыта считается нижняя выпавшая грань. Пусть события К, Б и Ч состоят в том, что на выпавшейграни присутствует соответствующий цвет. Тогда

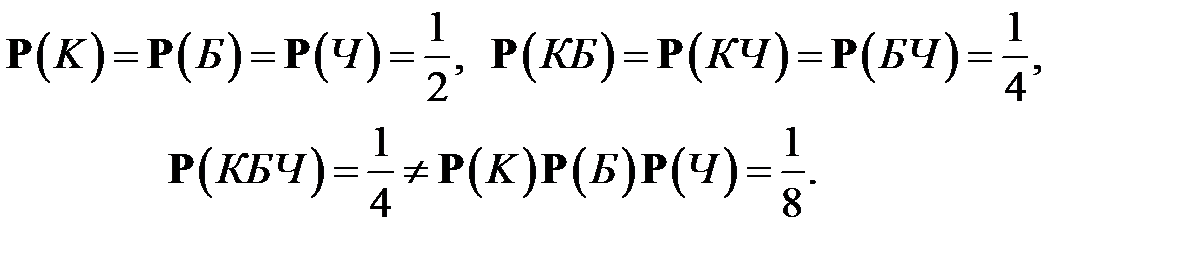
Таким образом, в данном случае события К, Б и Ч попарно независимы, но не являются независимыми в совокупности.

3. Формула полной вероятности.Вомногих случаяхвероятности случайных событий могут быть вычислены с помощью, так называемой, формулы полной вероятности. Пусть события 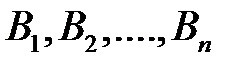(все 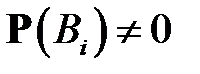) образуют полную систему. Тогда любое событие можно представить в виде следующей суммы несовместных событий

.

Отсюда

,

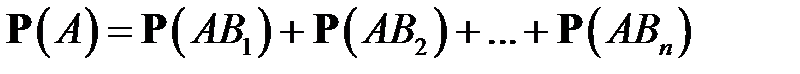и по формуле (1)

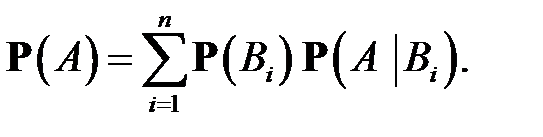(5)

Равенство (5) и есть знаменитая формула полной вероятности.События 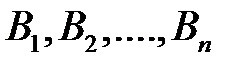обычно называют гипотезами. Таким образом,

если известны вероятности гипотез и условные вероятности события при различных гипотезах, то по формуле (5) можно вычислить безусловную вероятность этого события.

Если в равенстве

вероятность 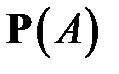заменить по формуле (5), то получим ещё одну важную формулу ТВ – формулу Байеса:

(6)

Эта формула позволяет пересчитывать априорные (т. е. до опыта) вероятности гипотез 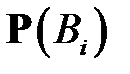после того, как произошло событие ( называют апостериорными, т. е. после опыта, вероятностями гипотез).

Рассмотрим несколько иллюстративных примеров на применение формулы полной вероятности.

Пример 7.Имеются две урны:в 1-й– 2 белых и 1 чёрный шар, во 2-й – 1 белый и 1чёрный шар. Из случайно выбранной урны наугад вынимается шар. Найти вероятность события A = {вынут белый шар}.

Р е ш е н и е. Здесь две гипотезы: – выбрана 1-я урна и – выбрана 2-я урна и, по условию, 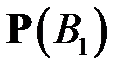= 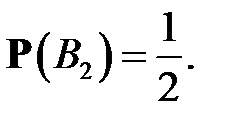Далее, по классической схеме,

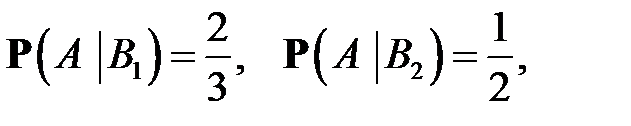
Следовательно, по формуле (5)

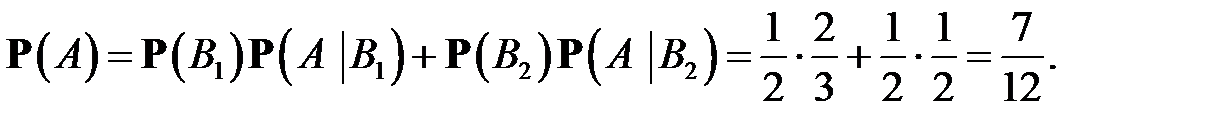
Пример 8.Изурны, содержащей М белых и N – М чёрных шаров, по схеме случайного выбора без возвращения последовательно извлекают двашара. Введём события A = {1-й шар – белый} и В = {2-й шар – белый}. Вычислить вероятность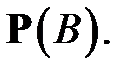

Р е ш е н и е. Здесь в качестве полной системы естественно взять события A и . По классической схеме имеем

Поэтому по формуле (5)

т. е. 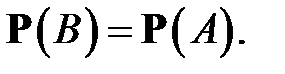Аналогично можно установить, что вынимая последовательно без возвращения шары, мы будем иметь одну и ту же вероятность вынуть белый шар на любом шаге. Тем самым, при жеребьёвке шансы всех участников одинаковы независимо от того, в какой очерёдности они тянут жребий.

Пример 9.Пусть имеются две урны с N шарами в каждой, при этом в 1-й урне 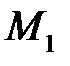белых шаров, а во 2-й – 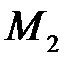белых шаров. Из случайно выбранной урны вынимается (с возвращением) n шаров. Рассмотрим событие A = {все вынутые шары – белые}. Здесь две гипотезы: – выбрана 1-я урна и – выбрана 2-я урна и, по условию, их априорные вероятности равны: 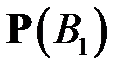= 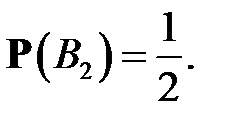Далее по классической схеме находим условные вероятности:

Формулы Байеса (6) дают нам апостериорные вероятности:

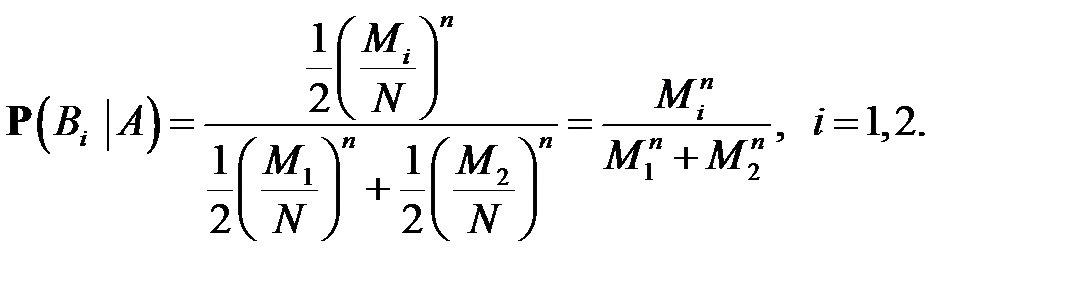
Если то при

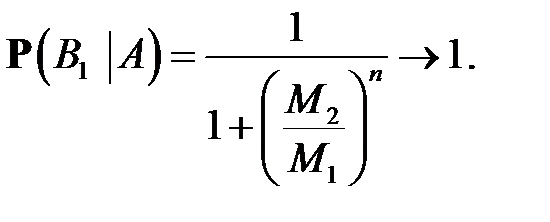
Но это означает, что выбор шаров наверняка был произведён из первой урны. Таким образом, знание исхода A такого эксперимента даёт возможность существенно скорректировать априорные сведения о гипотезах и .

4. Схема Бернулли.Важную роль в различных задачах ТВ играют схемы повторных независимых испытаний (т. е. когда вероятность того или иного исхода в каждом из них не зависит от исходов остальных испытаний, и испытания проводятся в неизменных условиях). Если в каждом испытании может наступить или не наступить некоторое событие A (обычно наступление A называют условно «успехом» (У), а наступление противоположного события – «неуспехом» (Н)), и если вероятность «успеха» в каждом испытании одна и та же, то такая схема называется схемой Бернулли[2]. Обычно обозначают 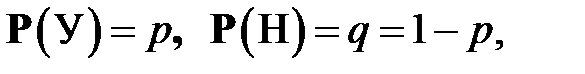и при этом предполагают, что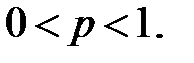

Примерами схемы Бернулли являются: стрельба по мишени (здесь испытание – отдельный выстрел), подбрасывание монеты или игральной кости (испытание – отдельное бросание), испытание электрических лампочек на длительность горения и т. д.

Для n испытаний схемы Бернулли элементарными событиями являются комбинации длины n из букв У и Н: 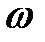=УУН…ННУ. Обозначим 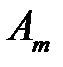событие, состоящее в том, что в этих испытаниях произошло ровно m «успехов». Поскольку испытания независимы, то вероятность каждой благоприятной (для события 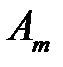) комбинации 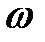равна 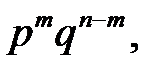а число всех таких комбинаций равно 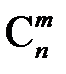(столькими способами можно зафиксировать те места в комбинации , на которых должны стоять буквы У), следовательно,

(7)

Мы пришли к уже встречавшемуся нам в схеме случайного выбора с возвращением (см. (1.8)) биномиальному распределению, так чтопримером схемы Бернулли является любая выборка с возвращением.

Схема Бернулли будет неоднократно встречаться нам в последующем изложении теории, в примерах и задачах.

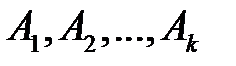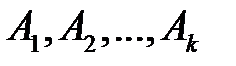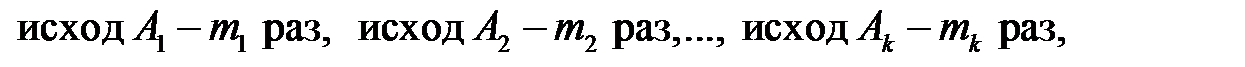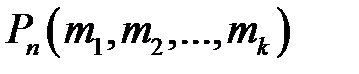Обобщением схемы Бернулли является полиномиальная схема, когда при каждом испытании возможно появление одного из k попарно несовместных исходов . Пусть (эти вероятности от испытания к испытанию не меняются). В этой схеме обычно интересуются вероятностью того, что в n испытаниях каждый из исходов произойдёт заданное число раз, скажем, при этом эти числа должны удовлетворять условию Вероятность такого события вычисляется по формуле

(8)

Набор чисел (8) называют полиномиальным распределением. При k = 2 это распределение сводится к биномиальному распределению.

При n подбрасываниях игральной кости мы имеем полиномиальную схему с k = 6 исходами и Если теперь «укрупнить» элементарные события, например, различать в каждом испытании только «6» и «не 6», то получим схему Бернулли с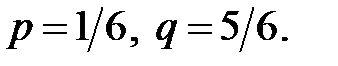

[1] Нумерация формул и примеров в каждом параграфе своя, при ссылке на формулу (пример) другого параграфа добавляется номер этого параграфа.

[2] Якоб Бернулли (1654 – 1705) – выдающийся швейцарский математик, один из основоположников теории вероятностей, впервые изучавший такую схему.