Связи b0 и b1 с другими описательными статистиками

Как задачи подбора «наилучшей» линии предсказания, так и измерения корреляции двух переменных касаются пары переменных для группы объектов. В обоих случаях данные можно представить на диаграмме рассеивания.

Есть несколько интересных соотношений между r_xy, s_x, s_y и коэффициентами b₀ и b₁ для прямой метода наименьших квадратов.

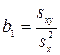, (8.8)

то есть b₁ равен ковариации X и Y, деленной на дисперсию X. Ковариация X и Υ для данных табл. 8.1 составляет 27,211, а = 38,408. Отношение s_xy/ = 0,708, значению b₁, найденному из уравнения (8.2).

Вспомните, что . Таким образом, если мы просто умножим это уравнение на

,

то получим b₁:

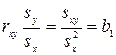. (8.9)

. (8.10)

Дисперсия предсказываемых значений, то есть значений 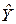, равна квадрату коэффициента корреляции X и Y, умноженному на дисперсию Y. Например, r_xy для данных табл. 8.1 равен 0,861; = 25,958. Поэтому дисперсия 20 предсказанных значений Y равна:

.

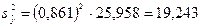Измерение нелинейных связей между переменными, корреляционное отношение η²

Этот параграф приведен здесь ради полноты и логической последовательности. Вы поймете его лучше после прочтения главы 15 об однофакторном дисперсионном анализе.

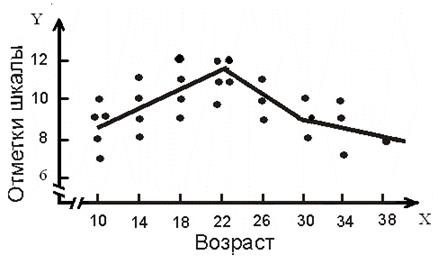
Рис. 8.4 – Связь между возрастом и характеристикой 28 людей
по вспомогательному тесту цифра-знак (WAIS)

Мы уже говорили, что произведение моментов Пирсона r измеряет лишь степень линейной связи между X и Y, теперь укажем еще описательную меру, применяемую в том случае, когда связь между X и Y преимущественно нелинейна. В качестве примера нелинейной связи рассмотрим данные рис. 8.4, показывающие связь возраста X с результатами Y вспомогательного теста цифра-знак шкалы интеллекта взрослых Векслера (WAIS). Данные рис. 8.4 представлены в табл. 8.2.

Из рис. 8.4 видно, что результаты растут линейно от 10 до 22 лет, достигают пика и затем довольно быстро уменьшаются.

Таблица 8.2

WAIS – Вспомогательный тест цифра-знак, располагающий по шкале оценки 28 лиц в восьми возрастных группах с равным шагом

Возраст с точностью до ближайшего года
Среднее возрастных групп: 8,60	9,50	10,50	11,50	10,00	9,00	8,67	8,00
Общее среднее всех значений =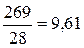

Мера линейной или нелинейной связи X и Υ обозначается η² (читается «эта в квадрате») и называется корреляционным отношением. Корреляционное отношение определяется так:

, (8.11)

где 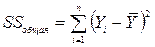, то есть сумма квадратов отклонений каждого значения Υ от среднего всех п значений Y, a SS_внутри получена следующим образом.

Для первого значения X находим отклонения соответствующих значений относительно их среднего и вычисляем сумму квадратов этих отклонений. Например, первая сумма квадратов в табл. 8.2 есть (7 – 8,60)² + (8 – 8,60)² + (9 – 8,60)² + (9 – 8,60)² + (10 – 8,60)². Этот процесс повторяется для каждого значения X. Так, для X = 14 имеем: (8 – 9,50)² + (9 – 9,50)² + (10 – 9,50)² + (11 – 9,50)². Для последней группы, Х = 38, сумма квадратичных отклонений значений Y относительно их среднего равна (8 – 8)² = 0, поскольку есть только одно значение. Наконец, складываем эти суммы квадратов отклонений для всех значений X. В результате имеем SS_внутри. (Если вы читаете этот раздел после главы 15, то обратите внимание, что SS_внутри есть «внутригрупповая сумма квадратов» в однофакторном дисперсионном анализе с неравными п).

Для данных табл. 8.2 величина SS_общая равна 54,68, а SS_внутри = 24,87. Отсюда значение 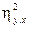есть

.

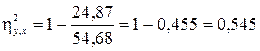Последующие соображения касаются интерпретации 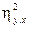. Коэффициент 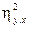– заметьте, что Y предшествует запятой, а X следует за ней, – является мерой степени предсказания Υ по X с помощью «наилучшим образом подобранной» линии, либо прямой, либо кривой.

Важно отметить, что 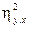и 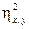обычно будут иметь разные значения. Это противоречит известным нам случаям, когда r_xy = r_yx. Мы можем смириться с фактом, что 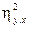может не быть равным 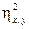, интуитивно обратившись к данным табл. 8.2. Если человеку 10 лет, то можно довольно уверенно предсказать, что его оценка по шкале цифра-знак равна ≈8,60. Однако, если известно, что оценка Y равна 8, то возраст X может быть как малым, около 10, так и большим, около 38 лет. Значит, можно довольно хорошо предсказать Y по X, но нельзя хорошо прогнозировать X по Y. Эти обстоятельства отражаются на величинах 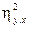= 0,545 и 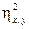, которую мы не вычисляли, но которая близка к нулю.

Величину 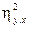надо сравнивать с 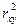, а не с 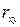. Мы знаем, что 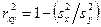, или

. (8.12)

Уравнение (8.12) показывает, что 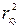(1 минус сумма квадратов отклонений Y относительно прямой предсказания) делится на 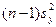. Уравнение (8.11) показывает, что 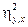(1 минус сумма квадратов отклонений Y относительно кривой предсказания, проходящей через средние значения Y для каждого значения X) разделен на 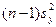. Кривая предсказания Υ по X показана на рис. 8.4.

Как и в случае 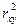, 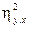должна быть меньше или равна единице и больше или равна нулю. Кроме того, 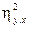≥ 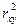. Разность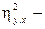 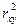является мерой степени нелинейности линии наилучшего сглаживания для предсказания Y по X.