Э л е м е н т а р н ы е с в о й с т в а б и н а р н ы х о т н о ш е н и й
1.Рефлексивность. Бинарное отношение R на множестве Х называется рефлексивным,если каждый элемент х множества Х находится в этом отношении сам с собой, т.е.
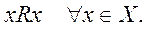
Пример. Если отношение R определить как «управлять», то свойство рефлексивности будет означать самоуправление или автоматическое управление.
2.Антирефлексивность. Бинарное отношение R на множестве Х называется антирефлексивным, если любой х из X не находится в этом отношении сам с собой, а R может выполняться только для несовпадающих элементов:
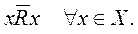
Пример. Если отношение R определить как «дополнять», то свойство антирефлексивности будет означать невозможность любого элемента x дополнять самого себя.
3. Симметричность. Бинарное отношение на множестве Х называется симметричным, если из того, что х находится в отношении R с у следует, что и y находится в этом отношении R с x, где x, у – любые элементы из Х:
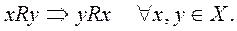
Пример. Если отношение R определить как «создавать сложную конструкцию», то свойство симметричности будет означать, что если любой элемент x создает сложную конструкцию в сочетании с элементом y, то и наоборот, любой элемент y создает сложную конструкцию в сочетании с элементом x.
4.Асимметричность. Бинарное отношение R на множестве Х называется асимметричным, если из того, что х находится в отношении R с у, следует, что y не находится в этом отношении R с x, где x, у – любые элементы из Х:
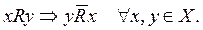
Очевидно, что асимметричное отношение R одновременно и антирефлексивно.
Пример. Если отношение R определить как «входить в состав сборочного узла», то из того факта, что элемент x входит в состав сборочного узла y, будет следовать, что обратное невозможно, поэтому такое отношение асимметрично.
5.Антисимметричность. Бинарное отношение R на множестве Х называетсяантисимметричным, если из того, что х находится в отношении R с у и y находится в этом отношении R с x для любых x, y следует, что x=y:
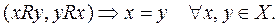
Пример. Фразу: «Благородный рыцарь сражается только с равным себе» можно трактовать как антисимметричность. Из того факта, что два рыцаря x и y сражаются между собой, следует, что они равны.
6.Транзитивность. Бинарное отношение R на множестве Х называется транзитивным, если из того, что х находится в отношении R с у, а y находится в этом отношении R с z, следует, что и х находится в отношении R с z для любых x, y, z из X:
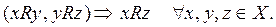
Пример. Пусть отношение R определено как «принадлежать к данной серии». Если установлено, что микросхемы x и y, а также y и z принадлежат к одной серии, то из этого следует, что микросхемы x и z также принадлежат к одной (данной) серии.
7.Отрицательная транзитивность. Бинарное отношение R на множестве Х называется отрицательно транзитивным, если транзитивно «отсутствие отношения» R:
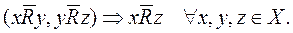
Пример. Пусть x, y и z – последовательные точки радиосхемы, а отношение R означает фильтрацию помех. Тогда, если помехи не отфильтрованы на участке схемы от точки x до точки y и от точки y до точки z, то это значит, что помехи не подавлены от x до z.
8.Сильная транзитивность. Бинарное отношение R на множестве Х называется сильно транзитивным, если оно одновременно транзитивно и отрицательно транзитивно:
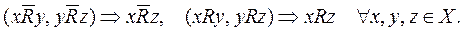
Пример. Пусть x, y и z – ретрансляционные станции, последовательно, по цепочке передающие сигналы, а отношение R соответствует передаче сигнала. Если сигнал передан от станции x к станции y и от станции y к станции z, то из этого следует, что сигнал передан от x к z. Обратный вывод справедлив в том случае, если сигнал не передан от станции x к станции y и от станции y к станции z: сигнал не передан от x к z.
Эти элементарные бинарные отношения являются основой для построения других, более сложных отношений.
Дата добавления: 2015-09-18; просмотров: 697;
