Поведение функции в окрестности существенной особой точки.
Теорема (Сохоцкого). Если  - существенная особая точка
- существенная особая точка 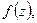 то
то 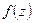 при
при 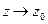 есть расширенная комплексная плоскость.
есть расширенная комплексная плоскость.
Доказательство. Т.е. надо доказать, что для 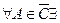 последовательность
последовательность 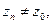
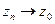 , т.ч.
, т.ч. 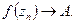
а) Частный случай 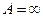 . Предположим противное, тогда
. Предположим противное, тогда 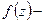 голоморфна и ограничена в
голоморфна и ограничена в  , тогда по теореме (30)
, тогда по теореме (30)  устранимая особая точка.
устранимая особая точка. 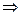 противоречие.
противоречие. 
б) Общий случай 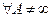 1) либо
1) либо 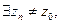
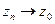 , т.ч.
, т.ч. 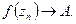
2) либо 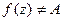 в некоторой проколотой окрестности точки
в некоторой проколотой окрестности точки  .
. 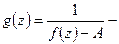 голоморфная в
голоморфная в  и
и  - существенная особая точка для g. f и g связаны ДЛО, тогда
- существенная особая точка для g. f и g связаны ДЛО, тогда 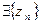 т.ч. (см. Пункт а) )
т.ч. (см. Пункт а) ) 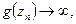 что равносильно тому, что
что равносильно тому, что 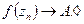
Дата добавления: 2015-09-02; просмотров: 815;
