Поведение функции в окрестности устранимой особой точки.

Теорема. Если: 1) 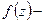голоморфна в .

2) 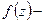ограничена в . То устранимая особая точка.

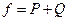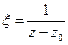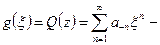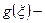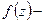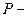Доказательство. Напишем ряд Лорана: . Исследуем главную часть: - замена переменных, тогда сходится в С (это ряд Лорана, т.к. 1/r – радиус сходимости). Таким образом голоморфна в С. Далее ограничена в и ограничена в 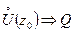ограничена в некоторой окрестности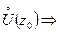 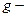ограничена в , тогда g ограничена в С. Тогда по теореме Лиувилля 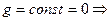все коэффициенты равны 0, тогда 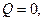т.е. это устранимая особая точка.