Определение. f – голоморфна в области D. – голоморфна в области в D. Тогда говорят, что – аналитическое продолжение функции f.

Замечание. Из теоремы единственности следует, что определение корректно, т.е. если аналитическое продолжение существует, то оно единственно.

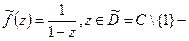Пример. одна голоморфная функция. другая голоморфная функция. Имеем 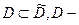единичный круг, вся плоскость без одной точки, 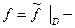имеем аналитическое продолжение (мы аналитически продолжили на всю плоскость и это продолжение !-но).