Определение.

Wavelet (WAVELET) переводится на русский язык как “короткаяилинебольшая волна”. Встречаются также и такие определения, как всплеск или маловолновая функция.

В качестве так называемых “материнских” вейвлетов (в Фурье-преобразовании “материнскими” являются набор синусов и косинусов) используются несколько десятков хорошо локализованных функций, порождающих путем растяжения и сдвига во времени целое семейство “дочерних” вейвлетов.

Далее “материнскую” функцию называем исходным вейвлетом, а порождаемые ими “дочерние” вейвлеты – базисными.

Пример исходных вейвлетов: Гауссов импульс; функция Хаара; вейвлет Марле; вейвлет Добеши.

Гауссов вейвлет V(x) – это вторая производная гауссова импульса y(x) = exp(–0.5x²), то есть

V(x) = (x² – 1)∙exp(–0.5x²) (8)

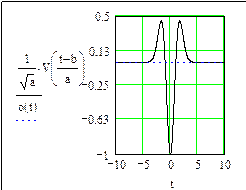
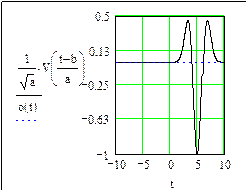
a =1, b = 0 a =1, b =5

Рис. 67. (начало)

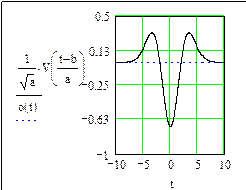
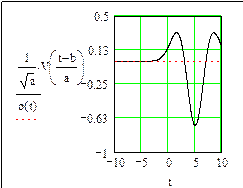
a =2, b = 0 a =2, b = 5

Рис. 67. (окончание)

Для вейвлета Хаара.

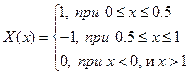(9)

Путем подстановки 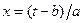и введения множителя 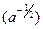от исходного вейвлета переходим к базисному.

Для двух представленных вейвлетов имеем:

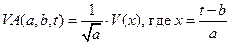. (10)

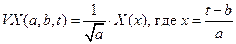(4)

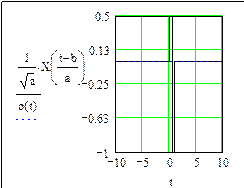
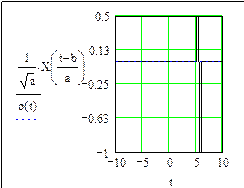
a =1, b = 0 a =1, b = 5

Рис. 68. (начало)

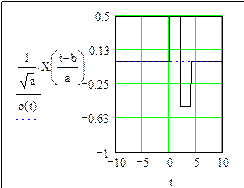
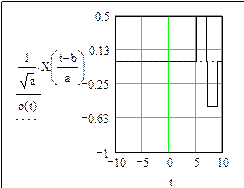
a =4, b = 0 a =4, b = 5

Рис. 68. (окончание)

При a = 1, b = 0 функции VA и XA являются “материнскими”. Из анализа графиков (см. рис. 67, 68) видно, что с увеличением параметра a импульс расширяется, а с изменением параметра b перемещается по оси времени t.

Основные признаки вейвлета: он имеет вид короткой, ограниченной во времени волны, расширяющейся или сжимающейся в зависимости от параметра a и перемещающийся по оси времени в зависимости от параметра b.

Кроме того, вейвлеты обладают следующими свойствами:

а) 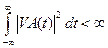– интеграл от квадрата модуля функции;

б) 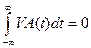- интеграл от самой функции, определяющей площадь, ограниченную графиком;

в) график материнской функции осциллирует вокруг нуля по оси времени;

г) все базисные вейвлеты имеют то же число осцилляций (около нуля), что и материнский.

Еще один пример вейвлета – Вейвлет Марле.

Исходный – “материнский” “марлет”:

,

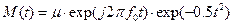где 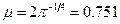- множитель, 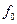– частота.

Базисная функция вейвлет-марлета, функция трех параметров a, b, :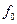

.

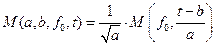А вообще в литературе встречаются следующие вейвлеты:

Хаара,

Симплета,

Добеши,

биортогональный,

ортогональный,

биортогональный сплайновый,

Мейера,

Гаусса,

Марле,

Шеннона,

Коифлета,

частотный В – сплайновый,

комплексный вейвлет Марле,

обратный ортогональный,

дискретная аппроксимация вейвлета Марле,

“мексиканская шляпа”,

комплексный Гаусса.

Итак, при изменении параметров b и a вейвлет движется по оси времени t и одновременно при этом расширяется. В силу данных свойств вейвлетов, используя их в качестве базисной функции, можно осуществлять частотно-временной анализ сложных сигналов, а не только частотный согласно Фурье-преобразованию.

В результате вейвлет-преобразование, то есть процедура, в основе которой лежит использование в качестве базисных функций вейвлетов, позволяет отслеживать локальные, как быстрые, так и кратковременные изменения в сигналах и преодолевать недочеты, свойственные Фурье-преобразованию. Особенно это важно для исследования коротких нестационарных процессов или одиночных импульсов сложной формы (например, одиночные модулированные импульсы РЛС).

По аналогии с Фурье-преобразованием имеем прямое и обратное вейвлет-преобразование:

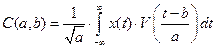(12)

– прямое V- преобразование;

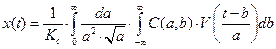(13)

– обратное V- преобразование,

где V(a,b,t) – функция, описывающая вейвлет (см. рис. 67), 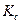– нормирующий коэффициент. Сравнивая V-преобразования и Ф-преобразования, устанавливаем различия между ними:

базисные функции sinωt и cosωt, зависящие от одного параметра – частоты ω, заменяются на вейвлет V(a,b,t) – функцию, зависящую от двух параметров a и b;

спектр S(ω), зависящий от одного параметра – частоты ω, заменяется спектрограммой, определяемой двухпараметрической функцией C(a,b), один из параметров которой (a) определяет частоту ω, другой (b) – время t.

Таким образом, в машинных алгоритмах, применяющих V-преобразования, принципиально требуются двумерные массивы.

При этом частотный анализ при Ф-преобразовании в виде функции S(ω) заменяется при V-преобразовании на частотно-временной анализ с помощью зависимости C(a,b), которую можно затем преобразовать к виду W(ω,t) (то есть получить “исходник”).

V-преобразование является более сложной вычислительной процедурой, чем Ф-преобразование, особенно при обратной задаче, то есть при синтезе сигнала, согласно выражению (13), поэтому V-преобразование особенно “притягательно” в тех случаях, когда сигнал является нестационарным процессом с локальными особенностями. К ним относятся сигналы, связанные с передачей речи и изображений. Таким образом V-преобразование не отменяет более простое в вычислительном отношении Ф-преобразование, а только дополняет его.

Пример непрерывного V-преобразования (как и в Ф-случае, здесь есть и дискретное V-преобразование). Тот же пример “двухчастотных” сигналов.

Вообще возможны следующие изменения параметров a и b:

линейный с изменением a и b с определенным шагом;

изменение по закону: 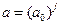; 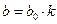, где 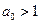, , 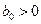j, k – целые числа;

изменение по закону 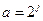, , 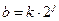где j, k – целые, при этом .

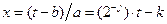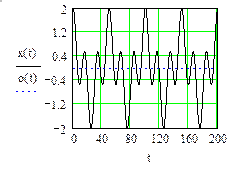
Рис. 69. (начало)

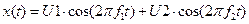– биения.

Применим Гауссово вейвлет-преобразование.

;

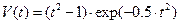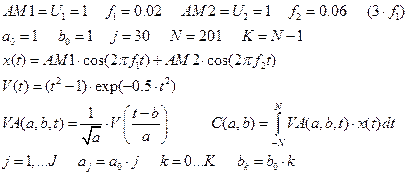
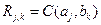– матрица с двумерным вейвлет-спектром.

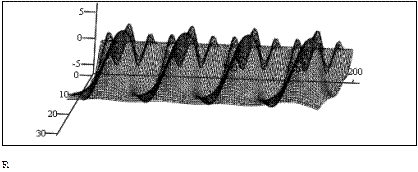
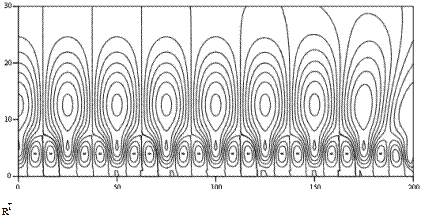
Рис. 69. (продолжение)

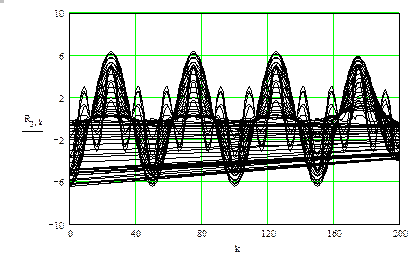
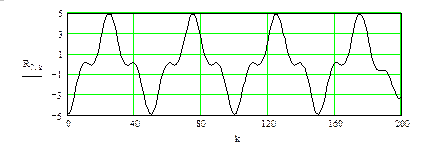Рис. 69. (окончание)

Для другого случая (сигнал с «переключением»).

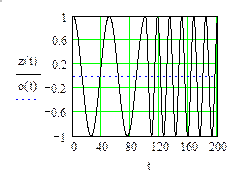
Рис. 70. (начало)

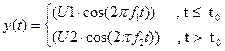
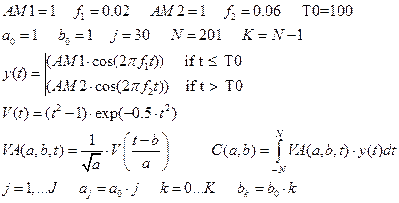
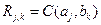– своя матрица с двумерным вейвлет-спектром.

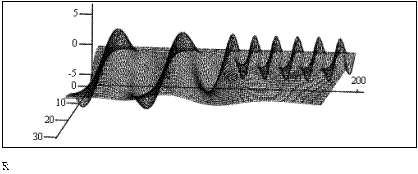
Рис. 70. (продолжение)

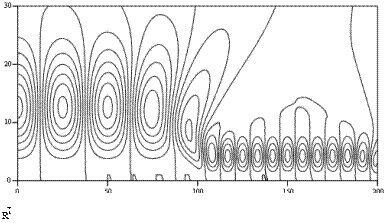
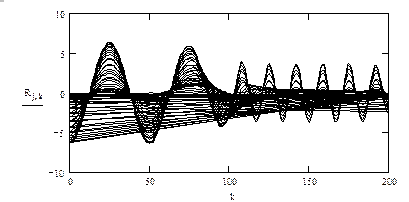
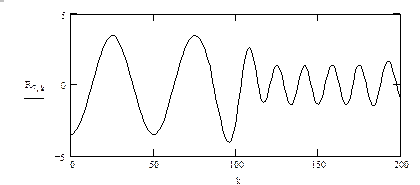Рис. 70. (окончание)

Таким образом, в разных сечениях (в аналогичных) есть уже существенная, то есть наглядная разница: появился инструмент, позволяющий при внешней схожести исходных спектров выявить локальные частотные или временные особенности исходных сигналов.

Где это наиболее важно:

1. Аудиоэкспертиза. Как различить (слушая по радио) голос Максима Галкина или Аллы Пугачевой? По радио (наше ухо как Фурье-анализатор) иногда почти невозможно. Если без шуток-аудиоэкспертиза (частотная) записанных образцов голосовых спектров приблизительно на 80–90 % дает недостоверный результат. А вот вейвлет-приемник (основное название гипотетического аппарата) помог бы наверняка отфильтровать характерные обертоны – причем не только по частоте, но и по времени, то есть по месту этого обертона в каждой звуковой фразе!

2. Исследование эхо-сигналов импульсных РЛС в случае постановки помех активными источниками помех. Например, такими активными постановщиками помех могут быть снабжены ложные фрагменты в МБР с разделяющимися боевыми частями. В этом случае “ошибка” в распознавании может обойтись очень дорого, например, в один город-миллионник или в область, или маленькую страну.

3. То же самое исследование эхо-сигналов при обнаружении движущихся (или неподвижных) подводных объектов, например АПЛ.

Вот где «овчинка стоит выделки» несмотря на сложность алгоритмов и большие мощности, и объемы памяти вычислительной техники применяемой при таком преобразовании.

Библиографический список

1. Головин О.В. «Радиоприемные устройства»,2004 год.

2. Зайзлер, Ежи «Системы передачи дискретной информации», 1970 год.

3. Левин Л.С., Плоткин М.А. «Цифровые системы передачи информации», М. 1982г.

4. Игнатов В.А. «Теория передачи сигналов и информации», М. 1979г.

5. Качанов В. И. Радиотехнические цепи и сигналы. Компьютеризированный курс.

Учебное пособие. – М.: ФОРУМ: ИНФРА – М, 2005. – 432 с. (Высшее образование).

6. Дьяконов В. MATLAB. Обработка сигналов и изображений. Специальный справочник – СПб.: Питер, 2002. – 608 с.: ил.

7. Кирьянов Д. В. Самоучитель MathCAD. 2001. – СПб.: БХВ – Петербург, 2002. – 544 с.: ил.

Оглавление

Классификация радиоприемных устройств (РПУ)

Общие сведения о принципах работы РПУ

Функциональные схемы РПУ

Супергетеродинный приемник

Основные показатели РПУ

Радиоприемники непрерывных сигналов

Прием однополосных сигналов

Приемники частотно-модулированных сигналов

Радиоприемники дискретных сигналов

Радиотелеграфные приемники

Импульсные приемники

Радиовещательные приемники

Профессиональные радиоприемные устройства декаметровых волн

Радиолокационные приемники

РПУ систем мобильной связи

Входные цепи РПУ

Усилители радиочастоты

Усилители промежуточной частоты (УПЧ)

Преобразователи частоты

Диодный преобразователь частоты

Балансные преобразователи частоты

Кольцевые ПРЧ

Транзисторные преобразователи частоты (ТПЧ)

Детекторы

Частотные детекторы

Фазовые детекторы(ФД)

Автоматические системы регулирования в РПУ

Системы АРУ (автоматической регулировки усиления)

Автоматическая подстройка частоты (АПЧ)

Введение в вейвлет - преобразования сигналов

Некоторые особенности Фурье – преобразования

Основные черты вейвлет – преобразования

Библиографический список