Векторная диаграмма. Гармонические колебания удобно представлять в виде векторных (круговых) диаграмм

Гармонические колебания удобно представлять в виде векторных (круговых) диаграмм. В этом случае гармоническое колебание совершает проекция радиус-вектора, равного по модулю амплитуде колебаний .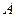

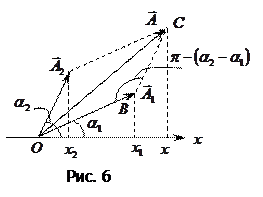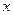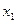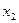Воспользуемся методом векторных диаграмм при сложении гармонических колебаний одинакового направления с одинаковыми частотами. Смещение колеблющегося тела равно сумме смещений и , которые записываются следующим образом:

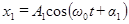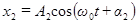и (16)

Представим оба колебания с помощью векторов 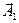и 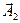(рис. 6). Построим по правилам сложения векторов результирующий вектор 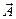. Легко видеть, что проекция этого вектора на ось 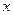равна сумме проекций слагаемых векторов 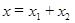. Следовательно, проекция вектора 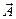представляет собой результирующее колебание.

Этот вектор вращается с той же угловой скоростью (циклической частотой) 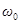, как и векторы 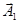и 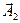, так что результирующее движение будет гармоническим колебанием с частотой 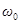, амплитудой 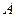и начальной фазой 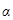. Из построения видно, что

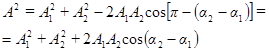(17)

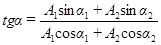. (18)

Итак, представление гармонических колебаний посредством векторов дает возможность свести сложение нескольких колебаний к операции сложения вращающихся векторов.

Проанализируем выражение (17) для амплитуды:

а) если разность фаз колебаний 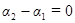, т.е. колебания происходят в одинаковой фазе, то амплитуда результирующего колебания равна ;

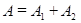б) если разность фаз колебаний 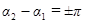, т.е. колебания находятся в противофазе, то амплитуда результирующего колебания .

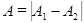Биения

Особый интерес представляет случай, когда два складываемых колебания одинакового направления малоотличаются по частоте. Результирующее движение при этих условиях можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такое колебание называется биением.

Пусть частота одного колебания 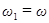, а частота второго колебания 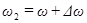, причем, 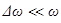. Амплитуды обоих колебаний полагаем одинаковыми и равными 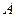. Для упрощения расчетов полагаем начальные фазы колебаний равными нулю. Тогда уравнения складываемых колебаний будут иметь следующий вид:

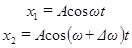
Складывая эти выражения и применяя тригонометрическую формулу для суммы косинусов 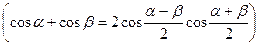, получаем 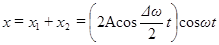(19).

(во втором множителе пренебрегли членом 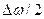по сравнению с ).

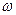График функции (19) для случая 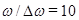изображен на рисунке 7.а.

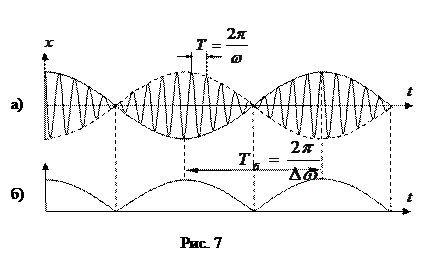Заключенный в скобки множитель в формуле (19) изменяется гораздо медленнее, чем второй множитель, так как 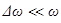. Это дает нам основание рассматривать колебание (19) как гармоническое колебание частоты , амплитуда которого изменяется по некоторому закону. Выражением этого закона не может быть множитель, стоящий в скобках, так как он изменяется от 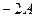до 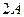, в то время, как амплитуда по определению – величина положительная. График амплитуды показан на рис 7.б. Аналитическое выражение амплитуды, очевидно, имеет вид:

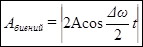. (20)

Функция (20) – периодическая функция с частотой в два раза превышающей частоту выражения, стоящего под знаком модуля, т.е. с частотой 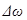. Заменяя в выражении (19) амплитуду через значение (20), получаем уравнение биений:

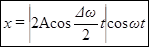(21)