Допускаемые напряжения изгиба

Здесь коэффициент долговечности

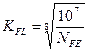
где 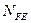= 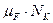. Величину N_FE ограничивают (10⁵= N_FE = 25∙10⁷).

Для материалов I и II групп:

;

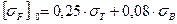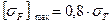
Для материалов IIIгруппы:

;

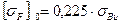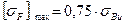
ВОПРОС 37 ПЛАНЕТАРНЫЕ ПЕРЕДАЧИ. ПРИНЦИП ДЕЙСТВИЯ. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОГО ОТНОШЕНИЯ.

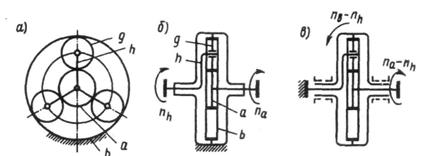
Планетарными называют передачи, содержащие зубчатые колеса с перемещающимися осями. Передача состоит из центрального колеса а с наружными зубьями, центрального колеса b с внутренними зубьями, водила h и сателлитов g.

Движение может передаваться

При неподвижном колесе b: от а к h или от h к а;

При неподвижном водиле h:от а к b или от b к а.

При всех свободных звеньях одно движение можно раскладывать на два или два соединять в одно, например от b к а и h, от а и h к b и т. п. в этом случае передачу называют дифференциальной.

Достоинствами планетарной передачи являются:

- широкие кинематические возможности;

- компактность;

- малая масса

- внутреннее зацепление (g и b) обладает повышенной нагрузочной способностью, так как у него больше приведенный радиус кривизны в зацеплении

- возможность получать большие передаточные отношения (до тысячи и больше) без применения многоступенчатых передач;

- малая нагрузка на опоры, так как при симметричном расположении сателлитов силы в передаче взаимно уравновешиваются.

К недостаткам планетарных передач относятся повышенные требования к точности изготовления и монтажа.

Кинематика планетарных передач

При исследовании кинематики планетарных передач широко используют метод остановки водила — метод Виллиса.

Всей планетарной передаче мысленно сообщается вращение с частотой вращения водила, но в обратном направлении. При этом водило как бы затормаживается, а все другие звенья освобождаются. Получаем так называемый обращенный механизм, представляющий собой простую передачу, в которой движение передается от а к b через паразитные колеса g. Частоты вращения зубчатых колес обращенного механизма равны разности прежних частот вращения и частоты вращения водила.

Для обращенного механизма:

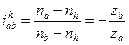
В нашем случае колесо b заторможено, а ‑ ведущее и h ‑ ведомое, при 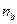= 0получаем:

;

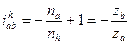
или

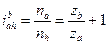
Частоту вращения сателлита определяют из равенства:

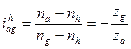
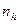При заданных и определяют 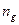или ( 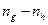)как частоту вращения сателлита относительно водила или относительно своей оси (используют при расчете подшипников).

ВОПРОС 38. СИЛЫ В ЗАЦЕПЛЕНИИ ПЛАНЕТАРНОЙ ПЕРЕДАЧИ. РАСЧЕТ НА ПРОЧНОСТЬ ПЛАНЕТАРНОЙ ПЕРЕДАЧИ.

Силы в зацеплении

По условиям равновесия сателлита:

и ,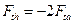

где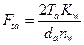

Здесь 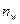‑ число сателлитов;

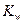‑ коэффициент, учитывающий неравномерность распределения нагрузки между сателлитами.

Радиальные и осевые силы при известной окружной силе определяют так же, как и в простых передачах.

Значение 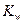зависит от точности изготовления и числа сателлитов.

Расчет на прочность.

Для расчета прочности зубьев планетарных передач используют те же формулы, что и при расчете простых передач. Расчет выполняют для каждого зацепления;

- для наружного зацепления ‑ колеса а и g,

- для внутреннего ‑ колеса g и b.

Так как силы и модули в этих зацеплениях одинаковы, а внутреннее зацепление по своим свойствам прочнее наружного, то при одинаковых материалах достаточно рассчитывать только зацепление колес а и g.

При разных материалах расчет внутреннего зацепления выполняют с целью подбора материала колеса или как проверочный.

При расчете на изгиб используют формулу.

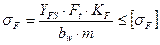
Для расчета по контактным напряжениям в расчётных формулах учитываются число сателлитов 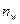и коэффициент 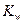неравномерности распределения нагрузки между ними. Например, формулу для проектного расчёта относительно делительного диаметра при К_На = 1 получим в виде

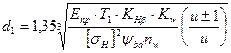
При расчете пары а ‑ g по формуле полагают, что 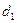‑ диаметр меньшего колеса пары, а и равно отношению чисел зубьев большего колеса к числу зубьев меньшего.

Для планетарных передач рекомендуют