Конденсаторы. Уединенные проводники имеют небольшую емкость
Уединенные проводники имеют небольшую емкость. Однако в технике используются устройства, обладающие электроемкостью до нескольких фарад. Такими устройствами являются конденсаторы. В основе принципа устройства конденсаторов положен тот факт, что при приближении к уединенному заряженному проводнику другого (даже незаряженного) проводника электроемкость системы значительно возрастает. В поле уединенного проводника на приближающемся теле возникают индуцированные заряды, причем заряды знака, противоположного сообщенному уединенному проводнику, располагаются к нему ближе и сильней влияют на его поле. Потенциал проводника по модулю уменьшается, а заряд сохраняется. Это означает, что его электроемкость растет.
Удаленные части приближающегося проводника можно соединить с Землей (заземлить), чтобы индуцированный заряд того же знака, что сообщенный уединенному проводнику, распределился по поверхности Земли и не оказывал влияния на потенциал системы. Очевидно, что, максимально приблизив противоположно заряженные проводники, можно достичь заметного увеличения электроемкости. Соответственно конденсаторы изготавливают плоскими, когда противоположно заряженные проводники (обкладки конденсатора) в виде, например, полосок фольги, разделяют тонким слоем диэлектрика. В этом случае электрическое поле системы оказывается сосредоточенным в пространстве между обкладками, и внешние тела не оказывают влияния на емкость конденсатора. Можно представить также обкладки в виде концентрических цилиндров или сфер.
Электроемкостью конденсатора, по определению, называется величина отношения заряда каждой из обкладок 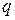 к разности потенциалов между ними:
к разности потенциалов между ними:
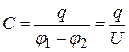 .
.
где 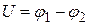 называется напряжением между обкладками.
называется напряжением между обкладками.
Напряженность электрического поля между двумя плоскостями, заряженными одинаково по модулю, но противоположно по знаку определяется соотношением:
 .
.
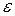 - диэлектрическая проницаемость материала между обкладками конденсатора.
- диэлектрическая проницаемость материала между обкладками конденсатора.
Умножив напряженность поля на расстояние между обкладками конденсатора 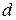 , получим разность потенциалов
, получим разность потенциалов 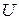 между обкладками:
между обкладками:
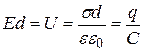 .
.
Если площадь пластин конденсатора равна 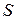 , то поверхностная плотность заряда
, то поверхностная плотность заряда
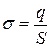 .
.
Тогда из соотношения (16.9) получаем:
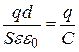 .
.
Следовательно емкость плоского конденсатора определяется формулой:
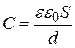 .
.
Дата добавления: 2015-09-14; просмотров: 1320;
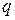 к разности потенциалов между ними:
к разности потенциалов между ними: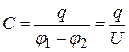 .
.
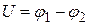 называется напряжением между обкладками.
называется напряжением между обкладками. .
.
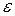 - диэлектрическая проницаемость материала между обкладками конденсатора.
- диэлектрическая проницаемость материала между обкладками конденсатора.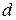 , получим разность потенциалов
, получим разность потенциалов 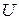 между обкладками:
между обкладками: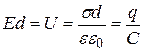 .
.
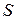 , то поверхностная плотность заряда
, то поверхностная плотность заряда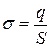 .
.
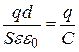 .
.
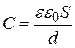 .
.
