ИСПОЛЬЗОВАНИЕ СУДЕЙ ДЛЯ ОТБОРА ПУНКТОВ В ШКАЛУ РАВНЫХ ИНТЕРВАЛОВ ТЕРСТОУНА
Выше мы рассмотрели процедуру фиксирования одномерного континуума. Но часто возникает прямо противоположная задача: нужно измерить субъективные отношения людей к весьма сложным явлениям, причем мы либо не можем, либо не желаем расчленять это отношение по составляющим его аспектам. Как и в построении шкалограмм, речь вновь идет о поиске латентной (скрытой) характеристики по ее внешним проявлениям, но цели поиска - иные.
Луи Тёрстоун [321] исходил из верной предпосылки, что психологическая установка человека на социальные объекты содержит эмоциональное отношение. Поэтому задача измерения сводится к тому, чтобы найти степень позитивной или негативной напряженности такого отношения. Процедура конструирования шкалы равных интервалов разрабатывалась Тёрстоуном по аналогии с процедурами поиска психофизиологических порогов восприятия.
Представим, что перед нами множество предметов одинакового внешнего вида, но незначительно отличающихся по весу. Перебирая предметы и взвешивая их поочередно на руке, определим минимальную величину, которая ощущается как разница двух близких весов. Это и есть интервал порога восприятия тяжести. Аналогичным образом строится процедура поиска субъективного порога различения оценочных суждений в шкале Тёрстоуна.
Разработка шкалы производится в несколько этапов.
(1) Вначале придумывается множество суждений позитивного и негативного характера, каждое из которых выражает отношение к некоторому объекту, явлению, социальной проблеме и т.п. - в зависимости от поставленной задачи. Например, это могут быть суждения, выражающие отношение к соблюдению законности: "Законы следует соблюдать во всех случаях"; "Бывают обстоятельства, когда нарушение определенного законодательного положения допустимо"; "Если бы наказания за несоблюдение законов были более строгими, нарушений бы не было"; "Я не очень беспокоюсь о нарушении закона, если никто об этом не сможет узнать" и т.д.
Суждения должны быть вполне однозначны и понятны, а главное, сформулированы так, чтобы с ними не могли согласиться люди, придерживающиеся прямо противоположных взглядов. Начальная численность таких суждений ориентировочно около 30. Для их формулировки можно привлечь представителей потенциальной аудитории опроса.
(2) Суждения, записанные на отдельные карточки, предлагаются "арбитрам", в качестве каковых выступают случайным образом отобранные представители опрашиваемой аудитории. Численность судей - около 50 человек.
(3) Этим арбитрам предлагается рассортировать все суждения одно за другим, последовательно в 11 групп, обозначенных буквами от А до Л. Возле картонки с буквой "А" надо положить суждения, в которых, по мнению арбитра, выражено максимально положительное отношение к данному объекту или явлению, а возле картонки с буквой "Л" - максимально негативное. Возле картонки с буквой "Е" должны помещаться суждения нейтрального, по мнению "арбитра", характера, а остальные - в зависимости от их содержания в промежутках от "А" до "Е" и от "Е" до "Л". Судей предупреждают, что не надо стараться распределить суждения по всем группам поровну, но только в зависимости от их смысла.

(4) После окончания сортировки начинается тщательный анализ, с тем, чтобы установить: (а) степень согласованности судейских решений и (б) "цену" каждого суждения на шкале в 11 интервалов (эта шкала найдена оптимальной).
Анализ распределения судейских оценок производится путем исчисления медианы и отклонений от медианной точки.
Подсчитаем судейские оценки для одного из суждений по табл. 5.
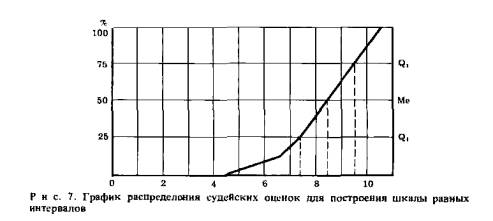
Имея такое распределение, построим график, где по вертикали отложим кумулятивный процент, а по горизонтали - шкалу из 11 интервалов. Кривая пересекает вертикали в точках, соответствующих медианной оценке для двух соседних пунктов на шкале. Поэтому они оцениваются дробями: 3,5 или 6,5, но не 3 или 6 (рис.7).
В районе 0 позитивный полюс, 5 - нейтральный, 11 - негативный.
Медианная оценка определяется по среднему перпендикуляру на базовую шкалу из 11 пунктов. Перпендикуляр опущен из точки, разделяющей ранжированный ряд судейских решений ровно пополам.
Цена суждения по медиане в нашем случае:
S = 8,5.
Определим, насколько единогласны судьи в своих решениях об этом суждении по квартальному отклонению (Q):
Q = 1/2 (Q3 - Q1 );
или для нашего примера:
Q= 1/2 (9,3 –7,3)=1,0
(5) В итоговую шкалу отбираются суждения, получившие наиболее согласованные оценки. Например, если имеются три суждения со сходной ценой (скажем, от 8,1 до 9,2) и с квартальными отклонениями, равными 1,0; 1,3; 1,5, то в итоговую шкалу отбирается суждение с Q = 1,0, как получившее наиболее согласованную оценку судей.
В окончательном виде шкала обычно содержит от 15 до 30 суждений, каждое из которых имеет "цену" или "вес", определенный по медиане судейских решений.
Очевидно, что, коль скоро арбитраж 50 судей позволил найти пороги различения между суждениями, шкалу можно признать метрической шкалой равных интервалов с отсчетом от 0.
(6) Для использования в массовом опросе все суждения тасуются в беспорядке. Опрашиваемые выражают согласие или несогласие с каждым из предложенных суждений. Цена суждения в опросном листе не проставлена: веса всех суждений записаны в инструкции по обработке данных.
(7) Индивидуальный ранг опрошенного по шкале Тёрстоуна определяется как медиана весов принятых им суждений. Например, в ответах некоего лица содержится всего четыре принятых суждения (все остальные им отвергнуты) с весами (5): 4,4; 4,8; 5,1; 5,6; 6,1. Тогда ранг индивида соответствует медианной оценке 5,1. Причет-ном числе принятых пунктов медианный ранг можно принять как среднеарифметическое интервала, в котором лежит медиана.
(8) Ранговая позиция группы опрошенных определяется как среднеарифметическая рангов всей совокупности, составляющей группу.
Обоснованность и устойчивость шкалы можно проверить с помощью уже известных нам приемов: использование независимого критерия, контроль по известной группе, повторное измерение с интервалом во времени.
Не обязательно начинать отбор суждений со столь большого числа вариантов, как это делал Тёрстоун. Наша практика показывает, что 30-50 суждений вполне достаточны для судейского отбора, после которого определится десяток вполне приемлемых пунктов шкалы. Также не обязательно вовлекать в работу очень большое число судей: можно получить статистически устойчивые данные на 50-60 экспертах.
Снижение точности замера за счет снижения дробности шкалы существенно повышает ее надежность. Если предлагать судьям расположить суждения не в 11, а в 5 интервалов, итоговая шкала будет более надежна, но менее точна. Выбор в пользу большей-меньшей точности зависит от предмета исследования и значимости гипотез, ;
а также от того, насколько точно измеряются в нем другие переменные. Если большинство переменных измеряется по трехчленным и пятичленным шкалам, но только одна — по 11-членной шкале, и притом все переменные подлежат взаимной корреляции, в этом случае повышенная точность 11-членной шкалы - излишняя роскошь. Она не оправдывается логикой сопоставления с другими переменными.
Работа с экспертами, аналогичная описанной выше, широко применяется и в других случаях, когда мы обращаемся к выборочной группе из массива обследуемых для того, чтобы глазами будущих испытуемых проверить соотносительную значимость оценок, придаваемых пунктам шкалы [219, с. 109-128].
Дата добавления: 2015-09-11; просмотров: 1561;
