Деформации при одноосном растяжении, сжатии
Различают: абсолютные деформации - это изменение размеров бруса до и после деформации, (удлинение 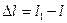 , сужение
, сужение 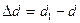 ); относительные деформации - это отношение абсолютной деформации к первоначальной длине, (продольная деформация
); относительные деформации - это отношение абсолютной деформации к первоначальной длине, (продольная деформация 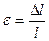 , поперечная деформация
, поперечная деформация 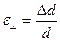 ).
).
Между относительными деформациями установлена связь в виде коэффициента Пуассона.
Коэффициент Пуассона 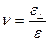 показывает во сколько раз продольная деформация больше поперечной. Для изотропных материалов может принимать значения от 0 до 0,5 ( 0 – пробка, 0,3 – сталь, 0,5 – резина)
показывает во сколько раз продольная деформация больше поперечной. Для изотропных материалов может принимать значения от 0 до 0,5 ( 0 – пробка, 0,3 – сталь, 0,5 – резина)
Между нагрузкой и удлинением английский ученый Роберт Гук установил прямо пропорциональную зависимость, которую впоследствии оформили в виде выражения 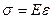 и назвали законом Гука :В пределахупругих деформаций нормальные напряжения при одноосном растяжении, сжатии прямо пропорциональны относительной продольной деформации. Коэффициент пропорциональности Е называется модулем продольной упругости или модулем Юнга, он характеризует жесткость материала, т.е. способность сопротивляться упругим деформациям (сталь - 2·105 МПа, медь - 1·105 МПа, резина – 5 МПа)
и назвали законом Гука :В пределахупругих деформаций нормальные напряжения при одноосном растяжении, сжатии прямо пропорциональны относительной продольной деформации. Коэффициент пропорциональности Е называется модулем продольной упругости или модулем Юнга, он характеризует жесткость материала, т.е. способность сопротивляться упругим деформациям (сталь - 2·105 МПа, медь - 1·105 МПа, резина – 5 МПа)
Коэффициент Пуассона и модуль продольной упругости – это упругие постоянные материала. определяются в лабораторной работе.
Механические свойства материалов:
- Характеристики прочности:
- предел пропорциональности σПЦ – это напряжение, до которого справедлив закон Гука;
- предел текучести σТ – это напряжение, при котором происходит рост пластических деформаций при практически постоянной нагрузке;
- предел прочности (временное напряжение) σПЧ, (σВ)– это условное напряжение, соответствующее максимальной нагрузке, выдерживаемой образцом до разрушения.
- Характеристики пластичности:
- относительное удлинение 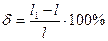 ,
,
- относительное сужение 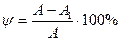 .
.
Характеристики прочности и пластичности определяются в лабораторной работе.
Условие прочности:
- по коэффициенту запаса 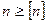 -Прочность элемента конструкции обеспечена, если рабочий коэффициент запаса не ниже допускаемого.
-Прочность элемента конструкции обеспечена, если рабочий коэффициент запаса не ниже допускаемого.
- по опасной точке 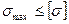 или
или 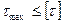 -Прочность элемента конструкции обеспечена, если максимальное рабочее напряжение не превышает допускаемое напряжение.
-Прочность элемента конструкции обеспечена, если максимальное рабочее напряжение не превышает допускаемое напряжение.
Виды расчетов и их цели:
- проверочный– проверить прочность спроектированного элемента конструкции:
- проектный -определить геометрические размеры проектируемого элемента конструкции:
- определение допускаемой нагрузки.
Условие прочности при растяжении, сжатии и виды расчетов:
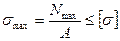 ,
,
где 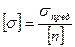 - допускаемое напряжение,
- допускаемое напряжение, 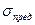 - предельное напряжение (пластичный материал -
- предельное напряжение (пластичный материал - 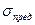 =
=  , хрупкий материал
, хрупкий материал 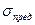 =
= 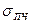 ),
), 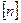 - допускаемый коэффициент запаса прочности.
- допускаемый коэффициент запаса прочности.
1. Проверочный 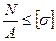
2. Проектный 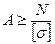
3. Определение допускаемой нагрузки 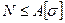
Задача 1.
1.1 Для стального стержня постоянного поперечного сечения (А = см2):
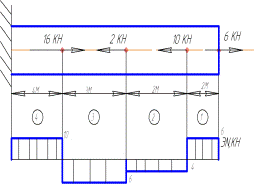
а) построить эпюру продольных сил (рис.1) Продольные силы на участках:
N1 =
N2 =
N3 =
N4 =
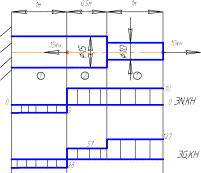
Рис.1 Расчетная схема стержня и эпюра продольных сил
б) определить опасный участок и напряжение на нем.
Примечание: Опасный участок это участок с максимальной нагрузкой или максимальным напряжением. В данной задаче опасный участок Nmax =
Напряжение на опасном участке
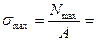
в) определить удлинение стального (Е = 2٠10 5 МПа) стержня
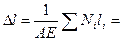
1.2 Для стального стрежня (Е = 2٠10 5 МПа) непостоянного поперечного сечения:
а) Продольные силы на участках:
N1 =
N2 =
N3 =
 МПа
МПа
Рис.2 Расчетная схема стержня и эпюры продольных сил и нормальных напряжений
б) Напряжения на участках:
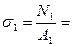
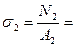
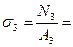
в) Опасный участок: 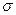 max =
max =
г) Удлинение 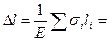
Задача 2. Проверить прочность стержня диаметром d = 10 мм, нагруженного растягивающими силами F = 10 кН, если допускаемое напряжение [σ] = 100 МПа.
Вид расчета - проверочный
Расчетная формула 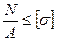
N =F =
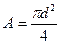 ;
; 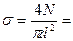
Вывод:
Задача 3. Определить диаметр стержня, нагруженного растягивающей силой F = 10 кН, если допускаемое напряжение [σ] = 100 МПа.
Вид расчета – проектный
Расчетная формула 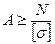 =
=
N =F =
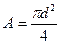 ;
; 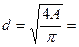
Задача 4. Определить допускаемую растягивающую нагрузку F на стержень диаметром d = 10 мм, если допускаемое напряжение [σ] = 100 МПа.
Вид расчета – определение допускаемой нагрузки
Расчетная формула 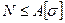 =
= 
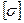 =
=
Дата добавления: 2015-09-11; просмотров: 4122;
