Пересечение геометрических тел
Линия пересечения поверхностей двух многогранников
(пирамиды и призмы)

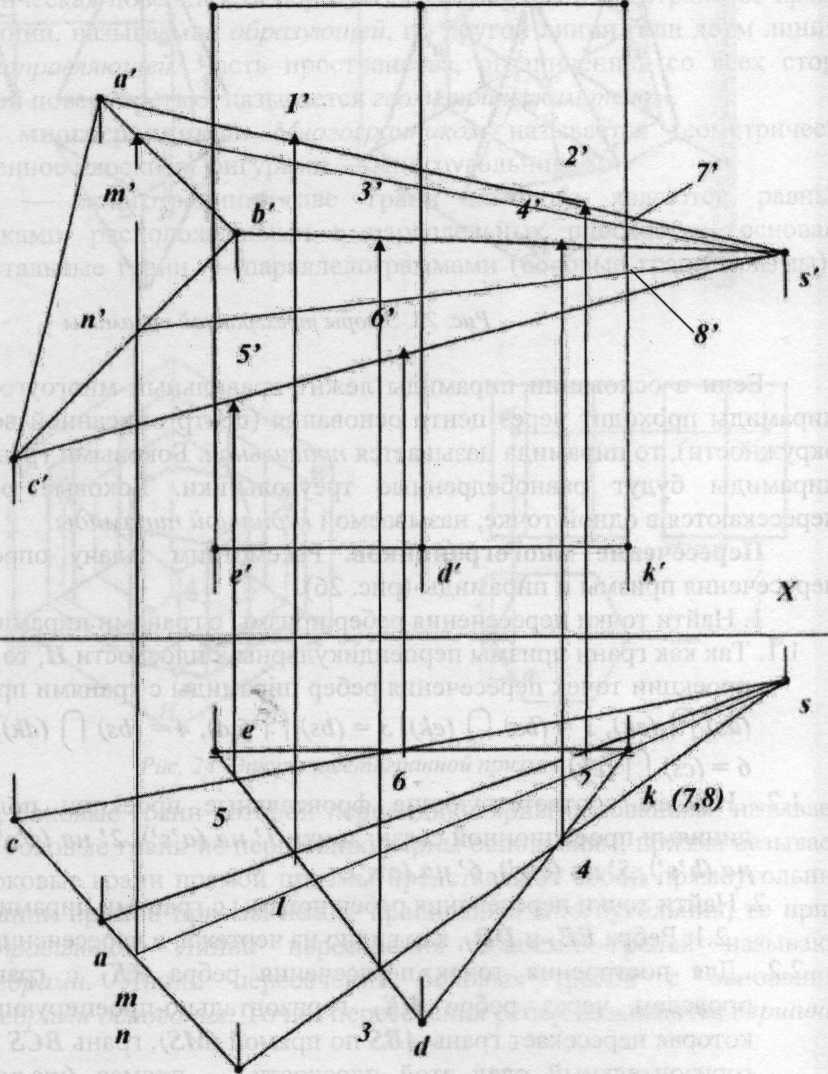
Линия пересечения представляет собой замкнутую ломаную пространственную или плоскую линию. Для построения линии пересечения нужно найти точки пересечения ребер каждого многогранника с гранями другого (или ребер одного с ребрами другого) и найденные точки соединить в определенной последовательности отрезками прямых.
Для определения точек пересечения ребер призмы с гранью пирамиды через ребра проведена горизонтальная вспомогательная секущая плоскостьPV, построена линия пересечения пирамиды и на линии пересечения ее с ребрами найдены искомые точки.
Пересечение призмы и пирамиды
e’1 d’1 k’1
b
В данном случае горизонтальная проекция линии пересечения поверхностей многогранников совпадает с горизонтальной проекцией призмы и найденные точки следует соединять только на фронтальной проекции. Для определения последовательности соединения фронтальных проекций точек, полученных в пересечении двух многогранников, используют метод Д.Г. Ананова. Он основан на построении схематических развёрток поверхностей пересекающихся тел. Рёбра призмы на схеме расположены вертикально, рёбра пирамиды – наклонно. На развёртки наносим точки, принадлежащие линии пересечения. Отметим на схеме знаком «+» те грани, которые на фронтальной плоскости будут видимы, а знаком «-» те грани, которые на этой плоскости будут невидимы. (Линии на гранях, где сочетаются два «минуса», будут невидимы).
| D |
| D’ |
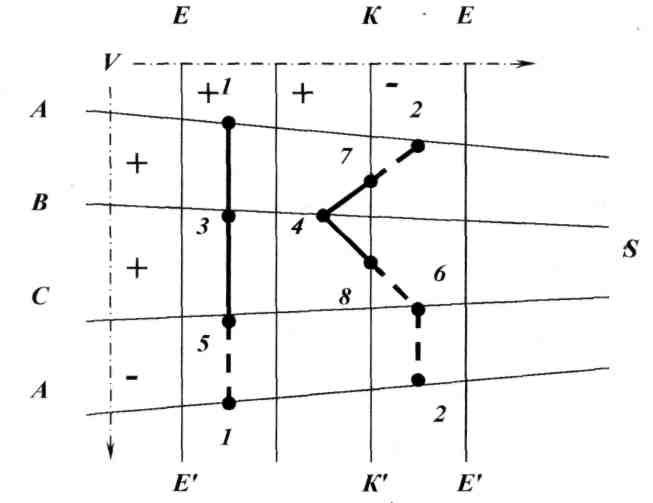
Соединим точки, лежащие на одной грани: точки 1 и 3, 3 и 5, 5 и 1 – лежат на грани EDE1D1, точки 2 и 7, 7 и 4 – лежат на грани ABS, точки 4 и 8, 8 и 6 – лежат на грани CBS точки 6 и 2 – лежат на грани ACS.
Определим видимость, используя правило: отрезки, принадлежащие двум видимым граням – видимы, отрезки, принадлежащие двум невидимым граням – невидимы, отрезки, принадлежащие двум разным по видимости граням – невидимы.
Отрезки 1-3, 3-5, 7-4, 4-8 – видимы, отрезки 5-1, 2-7, 8-6, 6-2 – невидимы.
На фронтальной проекции соединим отрезки согласно схеме, видимые отрезки – сплошными основными линиями, невидимые – штриховыми линиями.

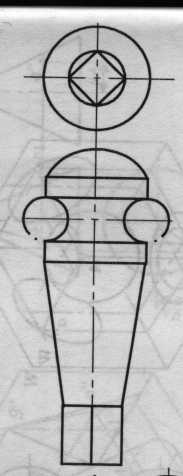
Пересечение многогранника и тела вращения
| PW |
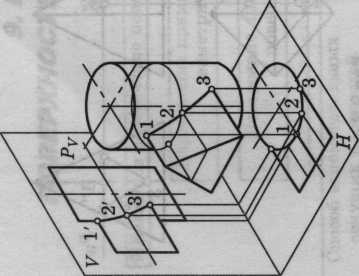
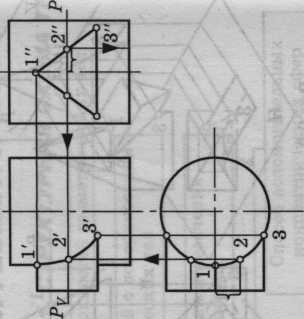
Пересечение тел вращения

Соосные поверхности вращения пересекаются между собой по окружностям
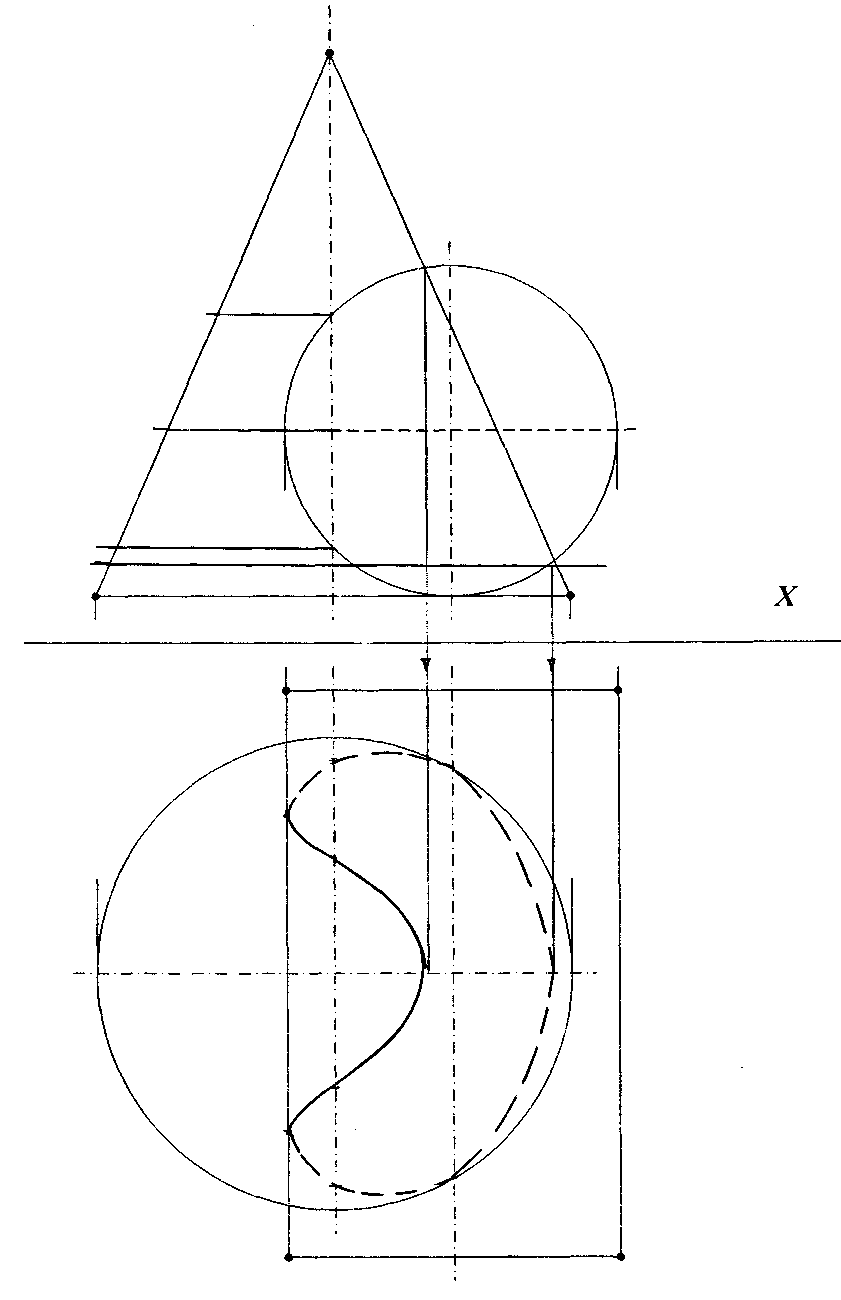
Если оси вращения поверхностей пересекаются и расположены параллельно одной из плоскостей проекций, то для построения линии взаимного пересечения используется способ вспомогательных секущих сфер

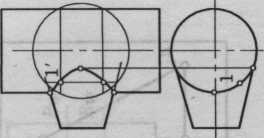
Пересечение конуса и цилиндра
| 31 |
| 41 |
| 61 |
| 51 |
| b |
| a |
| c |
| b’ |
| a’ |
| 3’ |
| 2’ |
| 21’ |
| 4’ |
| 41’ |
| 5’ |
| 51’ |
| 6’ |
| 61’ |
| 1’ |
| c’ |
Дата добавления: 2015-09-11; просмотров: 3888;
