Лабораторна робота 114. ДОСЛІДНА ПЕРЕВІРКА ЗАКОНУ ЗБЕРЕЖЕННЯ МОМЕНТУ ІМПУЛЬСУ
Завдання: перевірити експериментальним шляхом справедливість закону збереження моменту імпульсу.
Приладдя: установка, секундомір.
Теоретичний матеріал: кутова швидкість, момент сили та момент інерції, другий закон Ньютона для обертального руху, момент імпульсу, закон збереження моменту імпульсу, закон збереження енергії, робота сили.
Література:
1. Р.1. §§. 1.4 - 1.6; Р.3. §.3.5; Р.4. §§. 4.1 – 4.4;
2. Р.1. §§. 1.1 – 1.6; Р.4 §§. 4.1 – 4.4; Р.5. §§. 5.2; 5.11;
3. §§. 7.1 – 7.5; 7.7 – 7.12.
4. Р.4 §. 28 ; Р.5. §.§. 35 – 37;
5. §§.21 - 25.
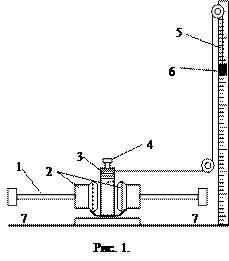 Опис установки. Основна частина установки – хрес-товина, яка може обертатися навколо вертикальної осі під дією моменту сили натягу нитки (рис.1). Нитку намотують на колонку 3, радіус якої є плечем сили. До нитки підвішують тягарець 6, положення якого можна відмічати за шкалою 5. Горизонтальний стержень хрестовини 1 закінчується упорами 7. По цьому стержні можуть вільно рухатися два тягарці 2. За допомогою гвинта 4 тягарці можна закріпити поблизу вертикальної осі хрестовини. У такому положенні тягарців хрестовина буде мати мінімальний момент інерції. Якщо тягарці розсунути до упорів, то це спричинить збільшення моменту інерції хрестовини. Під час опускання тягарця 6 з якоїсь висоти хрестовина буде обертатися зі сталим додатнім прискоренням (момент сили – стала величина). Після того, як нитка повністю розкрутиться з колонки 3 (тягарець 6 опуститься в нижнє положення), почнеться обертальний рух хрестовини з від’ємним кутовим прискоренням. Нитка знову буде намотуватися на колонку, а тягарець почне підніматися вгору. Якби не було втрат на роботу сили тертя, то тягарець повернувся б у попереднє положення. Знаючи висоту, з якої опускається тягарець, і висоту, на яку він піднявся, можна визначити роботу сил тертя. Це обчислення можна виконати для двох випадків: мінімального та максимального моментів інерції хрестовини.
Опис установки. Основна частина установки – хрес-товина, яка може обертатися навколо вертикальної осі під дією моменту сили натягу нитки (рис.1). Нитку намотують на колонку 3, радіус якої є плечем сили. До нитки підвішують тягарець 6, положення якого можна відмічати за шкалою 5. Горизонтальний стержень хрестовини 1 закінчується упорами 7. По цьому стержні можуть вільно рухатися два тягарці 2. За допомогою гвинта 4 тягарці можна закріпити поблизу вертикальної осі хрестовини. У такому положенні тягарців хрестовина буде мати мінімальний момент інерції. Якщо тягарці розсунути до упорів, то це спричинить збільшення моменту інерції хрестовини. Під час опускання тягарця 6 з якоїсь висоти хрестовина буде обертатися зі сталим додатнім прискоренням (момент сили – стала величина). Після того, як нитка повністю розкрутиться з колонки 3 (тягарець 6 опуститься в нижнє положення), почнеться обертальний рух хрестовини з від’ємним кутовим прискоренням. Нитка знову буде намотуватися на колонку, а тягарець почне підніматися вгору. Якби не було втрат на роботу сили тертя, то тягарець повернувся б у попереднє положення. Знаючи висоту, з якої опускається тягарець, і висоту, на яку він піднявся, можна визначити роботу сил тертя. Це обчислення можна виконати для двох випадків: мінімального та максимального моментів інерції хрестовини.
Установка дає змогу реалізувати рух зі змінним моментом інерції, а саме: під час опускання тягарця 6 хрестовина має мінімальний момент інерції (тягарці 2 містяться біля колонки); у нижньому положенні тягарця 6 тягарці 2 під дією відцентрової сили розлетяться до упорів 7, що спричинить різке зростання моменту інерції хрестовини. Тепер тягарець 6 буде підніматися під час обертання хрестовини з максимальним моментом інерції.
Виведення робочої формули.Основний закон динаміки обертального руху (рівняння моментів) визначає зв’язок між моментом зовнішніх сил 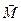 , що діють на тіло , та його моментом імпульсу
, що діють на тіло , та його моментом імпульсу 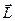 :
:
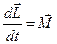 (1)
(1)
Для ізольованої системи, тобто системи, на яку не діють зовнішні обертальні моменти, отримаємо
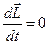 , тобто
, тобто 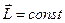 (2)
(2)
Ця рівність виражає закон збереження моменту імпульсу: момент імпульсу ізольованої системи не змінюється під час будь-яких процесів, що відбуваються у системі.
Під час обертання твердого тіла навколо нерухомої осі за відсутності моментів зовнішніх сил останній вираз набуває вигляду
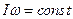 (3)
(3)
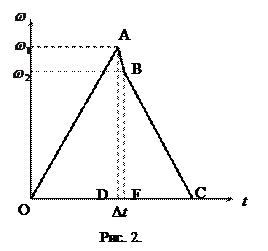 З виразу (3) видно, що зі зменшенням моменту інерції тіла
З виразу (3) видно, що зі зменшенням моменту інерції тіла 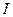 його кутова швидкість
його кутова швидкість 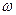 збільшується.
збільшується.
Наведемо графічно залежність кутової швид-кості хрестовини від часу, під час її руху зі змінним моментом інерції (рис. 2). Вітка ОА, що зростає, відповідає першій стадії, ВС – третій стадії. За незначний проміжок часу 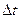 (відрізок DF) кутова швидкість різко змен-шується. Ділянка АВ відповідає стадії збільшення моменту інерції хрестовини. Застосовуючи закон збереження моменту імпульсу, відповідно, до (3), для нашого випадку
(відрізок DF) кутова швидкість різко змен-шується. Ділянка АВ відповідає стадії збільшення моменту інерції хрестовини. Застосовуючи закон збереження моменту імпульсу, відповідно, до (3), для нашого випадку
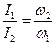 , (4)
, (4)
де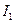 та
та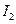 –відповідно, мінімальний та максимальний моменти інерції хрестовини;
–відповідно, мінімальний та максимальний моменти інерції хрестовини; 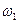 – найбільша кутова швидкість на першій стадії руху (точка А на графіку);
– найбільша кутова швидкість на першій стадії руху (точка А на графіку); 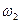 – найменша кутова швидкість на третій стадії руху (точка В на графіку).
– найменша кутова швидкість на третій стадії руху (точка В на графіку).
Визначимо величини, що входять у вираз (4), через інші, які можна безпосередньо виміряти на описаній установці.
Відношення моментів інерції визначимо за допомогою рівняння руху.
Поступальний рух тягарця, прикріпленого до нитки, описує рівняння
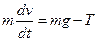 , (5)
, (5)
де 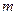 – маса тягарця, прикріпленого до нитки;
– маса тягарця, прикріпленого до нитки; 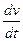 – його прискорення;
– його прискорення; 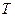 – сила натягу нитки;
– сила натягу нитки; 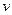 – швидкість поступального руху тягарця. Обертальний рух хрестовини описує основний закон обертального руху (1). У нашому випадку формула
– швидкість поступального руху тягарця. Обертальний рух хрестовини описує основний закон обертального руху (1). У нашому випадку формула
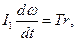 (6)
(6)
де 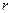 – радіус колонки, на яку намотана нитка;
– радіус колонки, на яку намотана нитка; 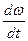 – кутове прискорення, пов’язане з лінійною залежністю
– кутове прискорення, пов’язане з лінійною залежністю
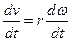 . (7)
. (7)
Визначивши з виразу (6) силу натягу 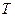 , підставивши його значення в (5) та скориставшись формулою (7) для лінійного прискорення тягарця (за умови
, підставивши його значення в (5) та скориставшись формулою (7) для лінійного прискорення тягарця (за умови 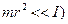 , отримаємо
, отримаємо
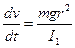 . (8)
. (8)
З іншого боку, під час рівноприскореного руху тягарця без початкової швидкості
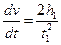 , (9)
, (9)
де 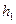 – висота, з якої опускається тягарець до повного розмотування нитки. З рівнянь (8) та (9) отримаємо
– висота, з якої опускається тягарець до повного розмотування нитки. З рівнянь (8) та (9) отримаємо
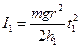 . (10)
. (10)
Аналогічно під час руху хрестовини з максимальним моментом інерції
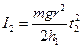 , (11)
, (11)
де 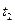 – час опускання тягарця з висоти
– час опускання тягарця з висоти 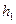 . З (10) та (11)
. З (10) та (11)
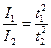 . (12)
. (12)
Отже, праву частину рівняння (4) ми уже виразили за допомогою величин, які безпосередньо визначаємо під час досліду.
Співвідношення кутових швидкостей визначаємо з закону збереження енергії.
У першій стадії під час опускання тягарця з висоти 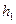
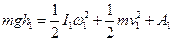 , (13)
, (13)
де 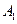 – робота сил тертя під час опускання тягарця. Скориставшись співвідношенням між лінійною та кутовою швидкостями
– робота сил тертя під час опускання тягарця. Скориставшись співвідношенням між лінійною та кутовою швидкостями 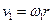 , при
, при 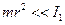 визначимо
визначимо
 . (14)
. (14)
Для всіх трьох стадій (опускання тягарця з висоти 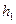 , піднімання його на висоту
, піднімання його на висоту 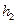 при змінному моменті інерції хрестовини) закон збереження енергії, вірогідно, виглядатиме так:
при змінному моменті інерції хрестовини) закон збереження енергії, вірогідно, виглядатиме так:
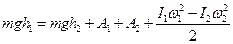 , (15)
, (15)
де 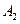 – робота сил тертя під час піднімання тягарця на висоту
– робота сил тертя під час піднімання тягарця на висоту 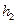 ; останній доданок – це енергія, яка перетворилася у тепло під час непружного зіткнення тягарців з упорами. З рівнянь (14) та (15)
; останній доданок – це енергія, яка перетворилася у тепло під час непружного зіткнення тягарців з упорами. З рівнянь (14) та (15)
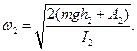 (16)
(16)
Тепер праву частину рівняння (4) можемо записати, використавши формули (14) та (16):
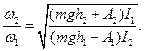 (17)
(17)
З рівнянь (4), (12) та (17)
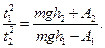 (18)
(18)
Виведемо вирази для 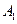 та
та 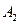 через величини, які безпосередньо вимірюємо під час досліду.
через величини, які безпосередньо вимірюємо під час досліду.
Нехай тягарець при найменшому моменті інерції 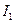 опускається з висоти
опускається з висоти 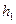 і піднімається на висоту
і піднімається на висоту 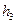 . Енергію, яка дорівнює різниці потенціальних енергій тягарця, витрачено на роботу сил тертя за весь час руху системи. Робота тільки під час опускання тягарця
. Енергію, яка дорівнює різниці потенціальних енергій тягарця, витрачено на роботу сил тертя за весь час руху системи. Робота тільки під час опускання тягарця
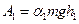 , (19)
, (19)
де 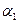 – величина, що показує, яка частина потенціальної енергії тягарця, піднятого на висоту
– величина, що показує, яка частина потенціальної енергії тягарця, піднятого на висоту 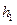 , витрачається на виконання роботи на подолання сил тертя під час його повного опускання.
, витрачається на виконання роботи на подолання сил тертя під час його повного опускання.
Значення 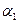 можна визначити за допомогою таких міркувань. Різниця потенціальних енергій тягарця на початковій
можна визначити за допомогою таких міркувань. Різниця потенціальних енергій тягарця на початковій 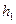 та кінцевій
та кінцевій 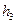 висотах повинна дорівнювати роботі сил тертя на повному шляху тягарця
висотах повинна дорівнювати роботі сил тертя на повному шляху тягарця 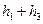 , яку за аналогією з (19) можна записати
, яку за аналогією з (19) можна записати
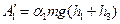 .
.
Отже,
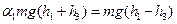 . (20)
. (20)
Звідси
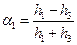 . (21)
. (21)
Аналогічно до формули (19) виразимо роботу, яку виконають сили тертя під час піднімання тягарця на висоту 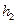 (згадаємо, що у цьому випадку система мала максимальний момент інерції
(згадаємо, що у цьому випадку система мала максимальний момент інерції 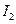 ):
):
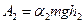 . (22)
. (22)
Щоб визначити коефіцієнт 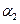 , використаємо ту частину експерименту, в якій тягарець опускався з висоти
, використаємо ту частину експерименту, в якій тягарець опускався з висоти 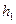 і піднімався на висоту
і піднімався на висоту 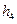 при максимальному моменті інерції. Аналогічно до (19)
при максимальному моменті інерції. Аналогічно до (19)
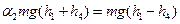 . (23)
. (23)
Звідси
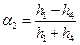 . (24)
. (24)
Підставивши формулу (21) у (19), а (24) у (22), отримаємо
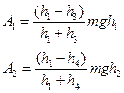 ; (25)
; (25)
Підставивши формулу (25) у (18) та виконавши елементарні перетворення, отримаємо робочу формулу для перевірки закону збереження моменту імпульсу:

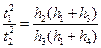 . (26)
. (26)
Позначимо ліву частину формули (26) 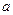 , праву –
, праву – 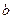 , тоді перевірка закону збереження моменту імпульсу зводиться до перевірки рівності
, тоді перевірка закону збереження моменту імпульсу зводиться до перевірки рівності
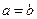 . (27)
. (27)
Дата добавления: 2015-09-11; просмотров: 2421;
