Лекция 2. Понятие о кватернионах
Кватернионы были введены в математику В.Р. Гамильтоном в 1843 году. Они представляют собой обобщение аппарата комплексных чисел на четырехмерный случай и записываются выражениями следующего вида:
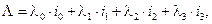
где 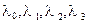 – произвольные действительные числа, называемые компонентами кватерниона
– произвольные действительные числа, называемые компонентами кватерниона 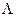 , а
, а  – кватернионные единицы.
– кватернионные единицы.
Кватернионное сложение определяется по правилам обычной векторной алгебры, т. е. при сложении двух кватернионов 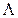 и
и 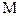 складываются их соответствующие компоненты
складываются их соответствующие компоненты 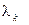 и
и 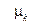 (
( 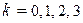 ).
).
Кватернионное произведение обозначается знаком « 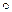 » и определяется следующими правилами умножения кватернионных единиц:.
» и определяется следующими правилами умножения кватернионных единиц:.
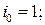
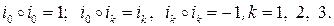
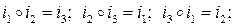
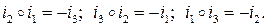
Нередко используется векторная интерпретация кватернионов. При этом элемент 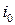 отождествляется с вещественной единицей, а элементы
отождествляется с вещественной единицей, а элементы 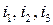 – с единичными векторами
– с единичными векторами 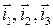 , образующими в трехмерном пространстве правую ортогональную тройку. Тогда умножение кватернионных единиц запишется через скалярное и векторное произведение следующей формулой:
, образующими в трехмерном пространстве правую ортогональную тройку. Тогда умножение кватернионных единиц запишется через скалярное и векторное произведение следующей формулой:
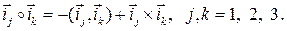
Исходя из этого, можно получить формулу для произведения двух кватернионов 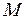 и
и 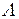 с ненулевой скалярной частью:
с ненулевой скалярной частью:
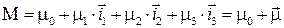 ;
;
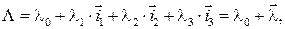
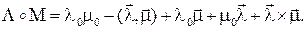 (2.1)
(2.1)
Рассмотрим основные свойства операций над кватернионами.
Итак, пусть 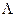 и
и 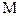 ‑ два различных кватерниона, причём
‑ два различных кватерниона, причём 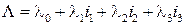 , а
, а 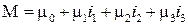 ,
, 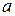 и
и 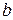 ‑ некоторые вещественные числа.
‑ некоторые вещественные числа.
1. Равенство кватернионов
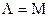 , если
, если 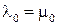 ,
, 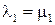 ,
, 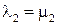 ,
, 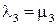 .
.
2. Правила сложения кватернионов
2.1. 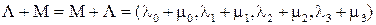 .
.
2.2. 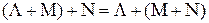 , где
, где 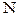 ‑ некоторый кватернион.
‑ некоторый кватернион.
3. Правила умножения кватернионов на число
3.1. 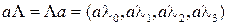 .
.
3.2. 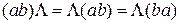 .
.
3.3. 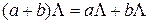 .
.
3.4. 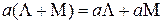 .
.
4. Правила перемножения кватернионов
Операция умножения кватерниона 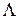 на кватернион
на кватернион 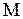 обозначается как
обозначается как 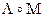 . Эта операция линейна, то есть, чтобы найти произведение двух кватернионов, достаточно найти, чему равно произведение скалярных и векторных составляющих кватерниона.
. Эта операция линейна, то есть, чтобы найти произведение двух кватернионов, достаточно найти, чему равно произведение скалярных и векторных составляющих кватерниона.
4.1. 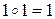
4.2. 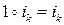
4.3. 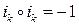
4.4. 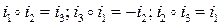
4.5. 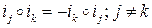
Мнимые единицы можно представить как орты трёхмерного пространства.
4.6. Найдём произведение двух кватернионов 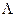 и
и 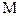 .
.
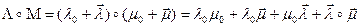 .
.
Найдём 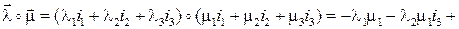
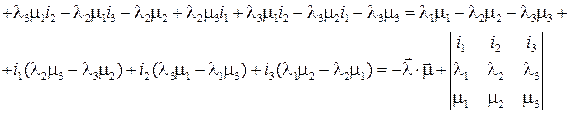
Итого, получаем: 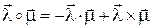 .
.
Сведя все результаты к одному, получаем:
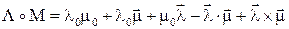
Теперь попытаемся найти 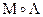 :
:
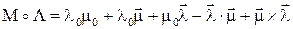
Из предыдущей формулы следует, что в общем случае 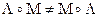 . Это обусловлено некоммутативностью векторного произведения
. Это обусловлено некоммутативностью векторного произведения 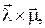 входящего в формулу для произведения двух кватернионов.
входящего в формулу для произведения двух кватернионов.
Кватернионы коммутативны, если векторные части коллинеарны.
Также отсюда следует, что 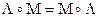 в двух случаях: если один из кватернионов является скаляром, либо если векторные части кватернионов пропорциональны, т.е. в тех случаях, когда векторное произведение
в двух случаях: если один из кватернионов является скаляром, либо если векторные части кватернионов пропорциональны, т.е. в тех случаях, когда векторное произведение 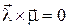 .
.
Найдём теперь составляющие произведения кватернионов.
Пусть 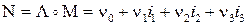 . Тогда из вывода формулы произведения кватернионов следует:
. Тогда из вывода формулы произведения кватернионов следует:
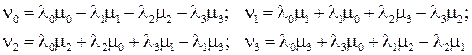 (2.2)
(2.2)
Умножение кватернионов обладает ассоциативными и дистрибутивными по отношению к сложению свойствами:
4.7. 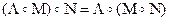
4.8. 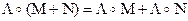
5. Сопряжённые кватернионы.
Кватернион 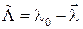 называется сопряжённым кватерниону
называется сопряжённым кватерниону 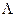 .
.
5.1. Кватернион, сопряжённый произведению 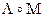 , равен
, равен
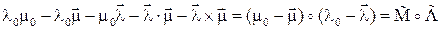 .
.
Это правило применимо для любого числа перемножаемых кватернионов.
6. Норма кватерниона. Нормой кватерниона называется
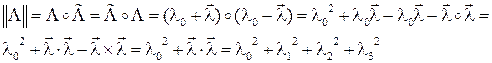
Если 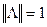 , кватернион называется нормированным.
, кватернион называется нормированным.
6.1. Норма произведения кватернионов
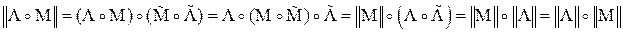
Это правило распространяется на любое число перемножаемых кватернионов.
7. Обратный кватернион.
Кватернион 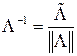 называется кватернионом, обратным
называется кватернионом, обратным 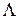 .
.
7.1. 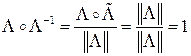
7.2. Пусть кватернион 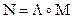 . Тогда
. Тогда 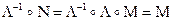 .
.
7.3. 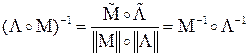 .
.
Это правило распространяется на любое количество перемножаемых кватернионов.
8. Существует тригонометрическая форма записи кватерниона.
Пусть 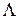 – нормированный кватернион, т.е.
– нормированный кватернион, т.е. 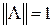 , а
, а 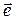 – единичный вектор, коллинеарный вектору
– единичный вектор, коллинеарный вектору 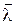 , тогда получаем тригонометрическую форму записи кватерниона
, тогда получаем тригонометрическую форму записи кватерниона
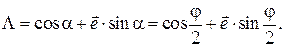
Нормированный кватернион описывает поворот тела, имеющего неподвижную точку. Поэтому его тригонометрическая форма выражается через параметры Родрига-Гамильтона.
Ненормированный кватернион
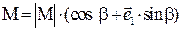
Дата добавления: 2015-09-11; просмотров: 3367;
