Аксонометричні проекції
Комплексне креслення на дві або три взаємно перпендикулярні площини проекцій має суттєвий недолік – відсутність наочності. Спосіб проекціювання, при якому предмет зображення жорстко зв’язується з просторовою декартовою системою координат, яка разом з предметом проекціюється центрально або паралельно на аксонометричну площину проекцій 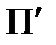 у заданому напрямі S, одержав назву аксонометричного, а отримане зображення називають аксонометрією.
у заданому напрямі S, одержав назву аксонометричного, а отримане зображення називають аксонометрією.
Напрямок проекціювання не повинен збігатися з напрямком хоча б однієї з осей декартової системи координат, тому отримане зображення матиме всі три виміри, що і надає йому наочність.
На рис. 2.2.1 наведено приклад проекціювання прямокутної декартової системи координат на площину аксонометричних проекцій 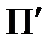 .
.
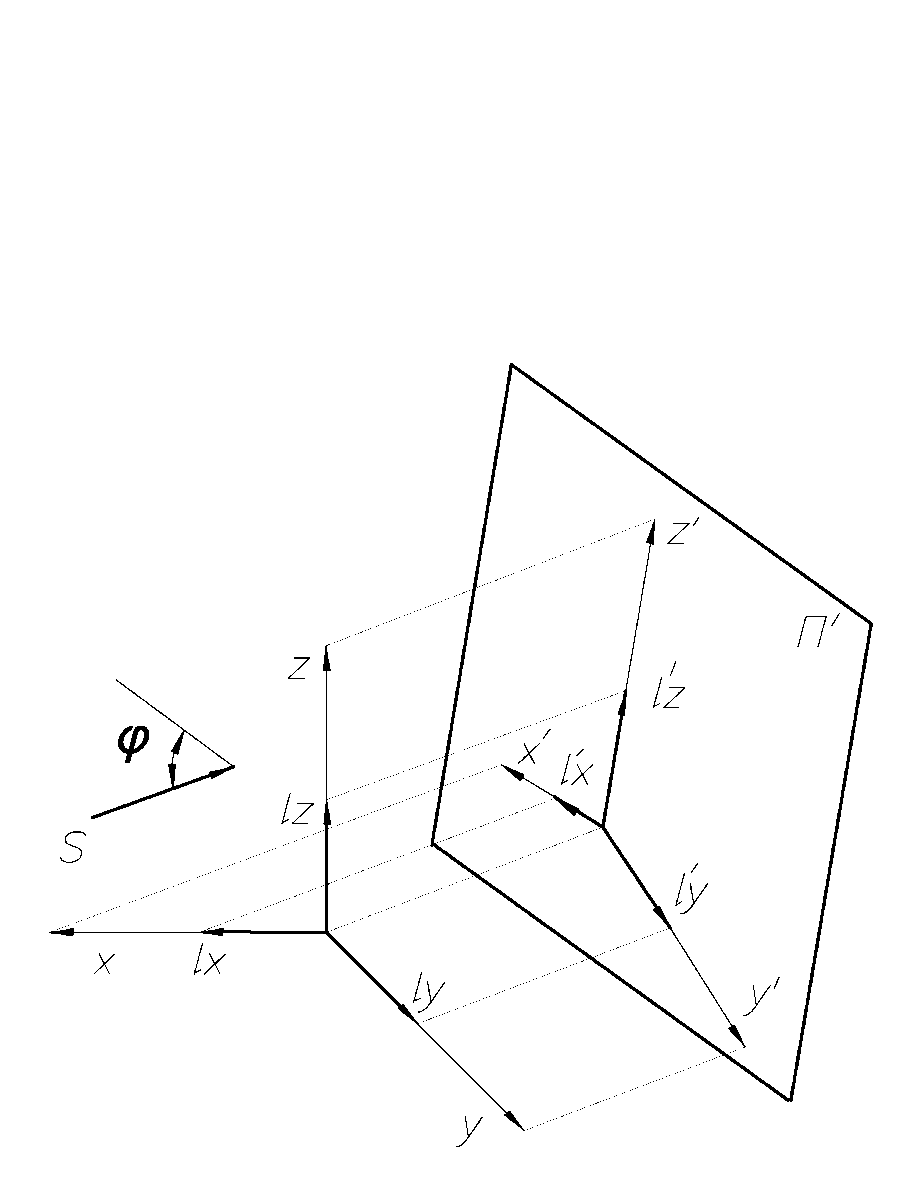
Рисунок 2.2.1
Залежно від напрямку S відносно 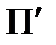 при паралельному проекціюванні аксонометрія може бути косокутною або прямокутною. На кожній із осей прямокутної декартової системи координат відкладемо від початку координат по одиничному відрізку
при паралельному проекціюванні аксонометрія може бути косокутною або прямокутною. На кожній із осей прямокутної декартової системи координат відкладемо від початку координат по одиничному відрізку 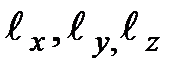 , кожен із яких проекціюється на аксонометричну площину проекцій
, кожен із яких проекціюється на аксонометричну площину проекцій 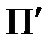 відповідним відрізком:
відповідним відрізком:
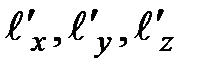 . Відношення аксонометричних проекцій до дійсних величин називають коефіцієнтами спотворень по трьох осях:
. Відношення аксонометричних проекцій до дійсних величин називають коефіцієнтами спотворень по трьох осях:
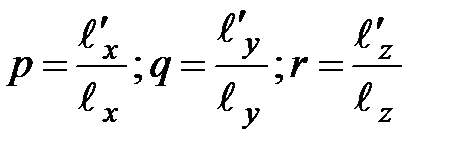 .
.
У прямокутній аксонометрії залежність між показниками спотворень виражають формулою:
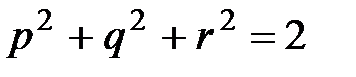 .
.
Якщо показники спотворень по всіх трьох осях однакові, тобто p = q = r, то аксонометрію називають ізометрією, якщо p = r 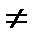 q, то аксонометрію називають диметрією, якщо p
q, то аксонометрію називають диметрією, якщо p 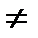 q
q 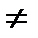 r, то аксонометрію називають триметрією.
r, то аксонометрію називають триметрією.
Дата добавления: 2015-09-11; просмотров: 974;
