И предпосылки для расчета по несущей способности
Балки работают на изгиб, который может быть прямым (простым) и сложным. Рассмотрим простейший случай прямого изгиба балки, когда внешние силы действуют в одной (вертикальной) плоскости и перпендикулярно к оси балки. Нагрузки могут
быть распределенными или сосредоточенными (сила, момент). В строительной практике наиболее распространены равномерно распределенные нагрузки. Для простоты рассуждений рассмотрим балку прямоугольного сечения (рис. 7.1).
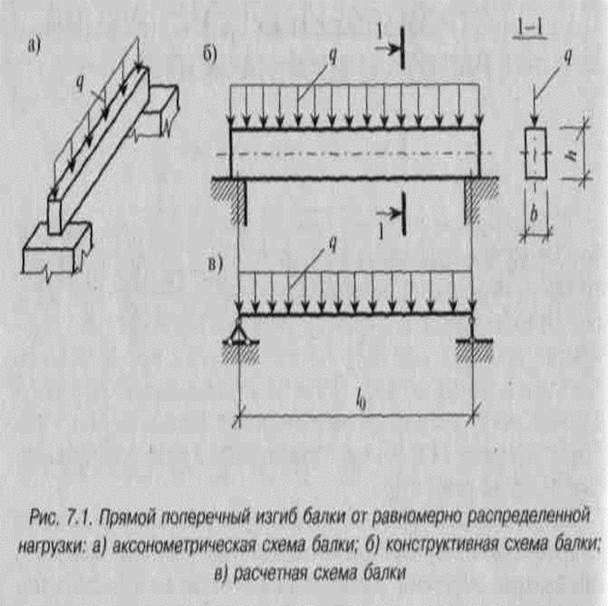
Если не принимаются специальные меры, т.е. балка свободно опирается на опоры, то одна опора считается шарнирно-неподвижной, а другая — шарнирно-подвижной (см. раздел 4).
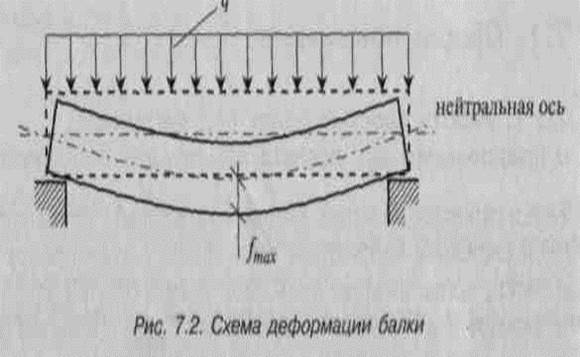
Из курса «Сопротивление материалов» известно, что прямой изгиб (рис. 7.2) характеризуется:
а) с геометрической точки зрения искривлением оси балки, удлинением растянутых (нижних) и укорочением сжатых (верхних) волокон. При этом нейтральная ось (слой) при искривлении свою длину не изменяет;
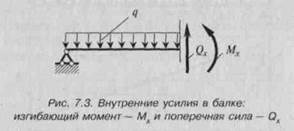
б) с точки зрения статики в любом сечении по длине балки возникают изгибающие моменты Мх и поперечные силы Qx (рис. 7.3).
|
| МХ и Qx определяются по правилам строительной механики, в зависимости от расчетной схемы балки и характера нагрузки (сосредоточенные, распределенные, моментные или их сочетания), путем построения эпюр, т.е. графиков изменения Мх и Qx по длине балки. Для случая действия равномерно распределенной нагрузки на простую балку по всей ее длине эпюры Мх и Q„ как известно из сопротивления материалов, выглядят, как показано на рис. 7.4, б, в. Наибольшие значения Мх и Qx при равномерно распределенной нагрузке определяется по формулам |

|
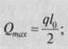
|
(7.1)
(7.2)
в) с тонки зрения напряженного состояния поперечный изгиб I характеризуется наличием нормальных, т.е. перпендикулярных к вертикальной плоскости сечения, напряжений а и касательных I напряжений т, лежащих в плоскости сечения. Нормальные напряжения изменяются по линейному закону по высоте сечения, достигая наибольших растягивающих (максимальных) значений атах I в крайних нижних волокнах (слоях) и наибольших сжимающих I значений в крайних верхних волокнах а„„л. По абсолютному значению они равны (ошм = а„„„).
Касательные напряжения (достигают наибольшего значения на уровне нейтрального слоя (оси х—х) и распределяются по криволинейному закону (параболе) — рис. 7.4, д, е.
Из рис. 7.4, г, видно, что нормальные напряжения ах достигают наибольших значений в середине балки, уменьшаясь влево и
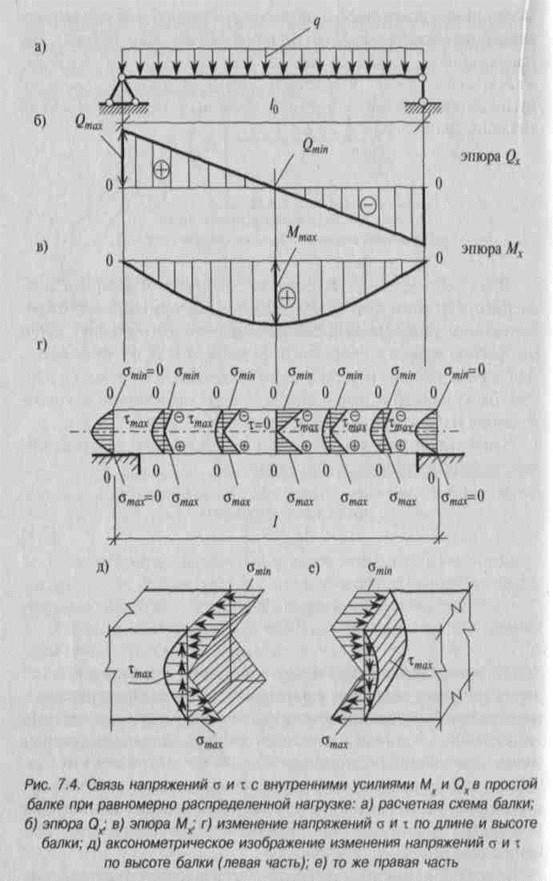
вправо от нее, и равны нулю на опорах. Касательные напряжения хх, наоборот, наибольших значений достигают на опорах и равны нулю в середине длины балки. Описанный характер изменения напряжений по длине балки зависит от изменения изгибающих моментов Мх и поперечных сил Qx. Нормальные напряжения ах напрямую зависят от изгибающего момента Мх, а касательные тх — от поперечной силы Qx. Для однородных и упругих материалов они могут быть найдены по формулам сопротивления материалов:
• нормальные напряжения в любом сечении балки
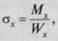 (7.3)
(7.3)
где Мх— изгибающий момент в рассматриваемом сечении балки; Wx — момент сопротивления относительно оси х—х, определяется по формулам сопротивления материалов; для профилей стального проката принимается по сортаменту (Приложение 1);
• касательные напряжения в любом сечении балки
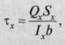 (7.4)
(7.4)
где Qx— поперечная сила в рассматриваемом сечении;
Sx— статический момент сечения, определяется по формулам или таблицам;
1Х — момент инерции сечения, определяется аналогично W„ Sx; b — ширина сечения балки.
Не останавливаясь на более подробных теоретических выводах, отметим, что, учитывая закон изменения изгибающих моментов Мх и нормальных напряжений можно установить рациональное (экономичное) очертание балки. Так, при равномерно распределенной нагрузке наиболее рациональной будет балка переменного по длине сечения, которая повторяет очертания эпюры М т.е. параболу. Учитывая характер изменения по высоте сечения I балки нормальных напряжений можно сделать вывод, что если I большая часть материала сосредоточена в крайних зонах сечения — I верхней и нижней, а минимум материала — в средней зоне, то I сечение получается наиболее рациональным; этому больше всего I соответствует двутавровое сечение.
Из вышесказанного следует, что расчет простых балок состоит I из проверки следующих двух условий:
1) нормальные напряжения ах в крайних слоях (волокнах) — нижнем и верхнем — не должны превышать расчетных сопротивлений материала на растяжение и сжатие:
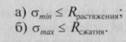 (7.5)
(7.5)
Из рис. 7.4, г, видно, что для балки постоянного по длине сечения достаточно выполнить условия (7.5) для сечения, находящегося в середине балки, где од. достигают наибольшего значения на всей ее длине;
2) касательные напряжения тх, которые достигают наибольших значений на уровне нейтрального слоя, не должны превышать расчетных сопротивлений материала сдвигу:
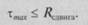 (7.6)
(7.6)
Для прямоугольных сечений при равномерно распределенной нагрузке касательные напряжения невелики из-за значительной ширины балки, но для балок двутаврового сечения, особенно при действии на них сосредоточенных нагрузок, такой расчет необходим.
Из рис. 7.4, г, видно, что в поперечных сечениях, расположенных между опорами балки и ее серединой, по длине балки одновременно возникают нормальные од. и касательные х^ напряжения. Их совместное действие может вызвать опасное напряженное состояние. Оно не опасно при равномерно распределенной нагрузке для прямоугольных сечений, выполненных из однородного материала, и прокатных стальных двутавров, в сортамент которых заложены такие размеры стенок, которые обеспечивают достаточную прочность. При сосредоточенных нагрузках в стальных и деревянных конструкциях, а для железобетонных конструкций и при действии равномерно распределенной нагрузки необходима проверка условий 7.6.
Дата добавления: 2015-09-02; просмотров: 1797;
