Двоично-кодированные счетчики с произвольным модулем счета

Нередко на практике необходимо создавать счетчики с модулями, не равным целой степени числа 2 — счетчи­ки с произвольным модулем. Из них наиболее часто встре­чаются двоично-десятичные счетчики, поскольку десятич­ная система счисления является общепринятой.

Для построения счетчика с произвольным модулем М число log₂M округляют до ближайшего большего целого числа

п > log₂M, п — целое. (3.31)

В результате получаем число необходимых триггеров. Основанием для счетчика с произвольным модулем служит двоичный счетчик, имеющий 2ⁿ состояний. Следователь­но, счетчик с произвольным модулем будет иметь L лиш­них неиспользуемых состояний, подлежащих исключению

L = 2ⁿ - М. (3.32)

Наибольшее распространение при построении таких счетчиков получили:

· метод исключения лишних состояний;

· метод управляемого сброса.

Первый метод основывается на алгоритме синтеза циф­рового устройства. При таком подходе составляется граф и таблица переходов-выходов, производится выбор исполь­зуемых триггеров. Затем составляется таблица истиннос­ти и минимизируется комбинационная схема. Получен­ное последовательностное устройство с памятью обладает схемой с однозначно определенными видами связи между отдельными элементами. Составление такой схемы целе­сообразно при проектировании устройств, выпускаемых большими партиями. Иначе первый подход экономичес­ки нецелесообразен.

Гораздо чаще на практике применяют метод управля­емого сброса. Для реализации данного алгоритма приго­ден любой двоичный счетчик, имеющий входы сброса и начальной установки. Идея метода состоит в принудительном формировании сигнала сброса триггеров разрядных схем двоичного счетчи­ка при появлении на его выходе кода, совпадающим с требу­емым модулем счета М. Рассмотрим схему на рис. 3.46.

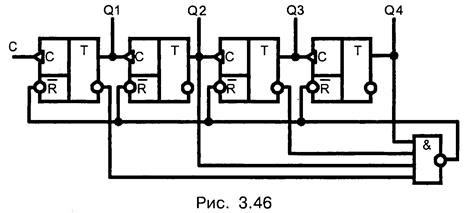
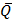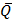Четырехразрядный двоичный счетчик имеет дополни­тельно четырехвходовый элемент 4И-НЕ, на входы кото­рого подаются сигналы с выходов триггера Q_{4 3}Q_{2 1}- При появлении на синхронизирующем входе С одиннадцатого по счету импульса триггера счетчика устанавливаются в состояние 1010

Q₄=1 Q₃= 0 Q₂=1 Q₁=0, (3.33)

что соответствует

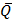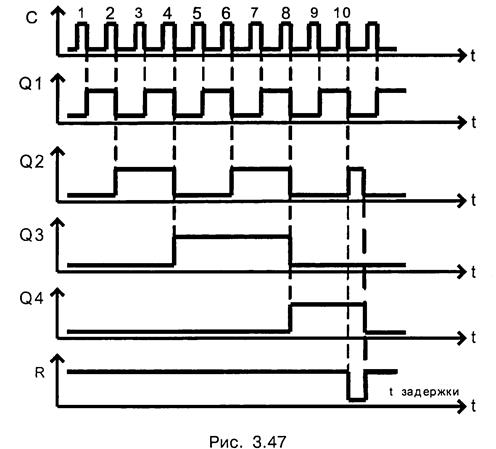
Q_{4 3}Q_{2 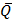1}= 1111. (3.34)

Тогда элемент 4И-НЕ через время, равное задержке распространения сигнала формирует на своем выходе ну­левой сигнал сброса, который, поступая на асинхронные входы R всех триггеров, принудительно устанавливает их в нулевое состояние. Далее начинается новый цикл счета.

Временные диаграммы, иллюстрирующие работу де­сятичного счетчика, представлены на рис. 3.47.

В методе управляемого сброса на короткое время, обус­ловленное задержкой t_3ad в элементах тракта 4И-НЕ и сраба­тыванием триггеров по входу обнуления R, в счетчике уста­навливается лишнее выходное состояние 1010 (рис. 3.47). Если такое явление даже кратковременное является недопу­стимым, то проектируют счетчик по методу исключения лишних состояний.

Решение задачи управляемого сброса можно упростить. Например, при формировании двоично-десятичного счет­чика обратим внимание, что единичные выходы берут с двух разрядов — второго и четвертого. Тогда можно использовать двухвходовый элемент 2И-НЕ, подавая на его входы сигналы Q₄ Q₂, а инверсные выходы с первого и третьего счетчиков 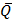_{1 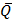3} не использовать.

По такому принципу строится десятичный счетчик на микросхеме К555ИЕ5, имеющий два входа асинхронного сброса (рис. 3.48, а), объединенных операцией И-НЕ. Для выполнения десятичного счета достаточно входы RO (1), RO (2) соединить с выходами Q₄ Q₂.

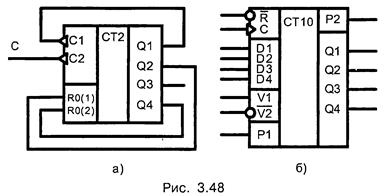
Ввиду особой важности десятичных счетчиков в стан­дартных сериях микросхем имеются десятичные счетчи­ки. Например, микросхема К555ИЕ9 (рис. 3.48, б) — четырехразрядный двоично-десятичный счетчик с асинхронным сбросом, дешифрирующим счетным выходом, с возможностью синхронной установки с произвольное со­стояние от нуля до девяти. Счетчик имеет вход синхро­низации С, вход установки нуля R, четыре информаци­онных входа D1-D4, входы разрешения счета VI, разре­шения предварительной записи V2, разрешения перено­са Р1, четыре выхода Q1-Q4 и выход переноса информа­ции Р2.

Для переноса импульса в следующий каскад предус­мотрена специальная схема с входом разрешения перено­са Р1 и выходом Р2. При подаче на вход схемы девятого счетного импульса на выходе Р2 появляется высокий уро­вень. После десятого импульса, когда счетчик обнуляет­ся, выход Р2 снова переходит в состояние низкого уров­ня. Следовательно, на каждые десять импульсов счета формируется один импульс переноса на вход счетчика стар­шего разряда.

Аналогичным образом могут быть построены счетчи­ки на любое другое значение модуля счета. Например, для построения счетчика по модулю 5 согласно (3.31) необхо­димо три триггера 3>log₂5. На рис. 3.49 показан пример счетчика по модулю 5.

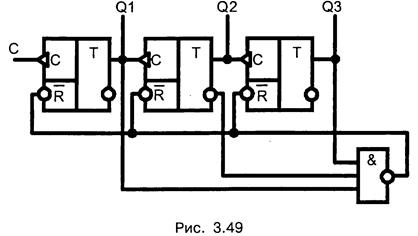
На входы элемента 3И-НЕ подаются сигналы Q₃Q₂Q₁ в соответствии с 5₁₀ = 101₂. Далее по приходу пятого им­пульса на выходе элемента ЗИ-НЕ формируется нулевой уровень, который обнуляет счетчик, поступая на входы асинхронного сброса R всех триггеров. Отметим, что среди других счетчиков с недвоичным ко­дированием практическое значение имеют счетчики с кодом Грея, счетчики Джонсона, счетчики с кодом «1 из N».