Способ замены плоскостей проекций. Сущность метода заключается в том, что при неизменном положении геометрической фигуры в пространстве одна из плоскостей проекций ( П1 или П2) заменяется на

Сущность метода заключается в том, что при неизменном положении геометрической фигуры в пространстве одна из плоскостей проекций ( П₁ или П₂) заменяется на новую ( П₄). Новая плоскость выбирается таким образом, чтобы:

1) не нарушался принцип перпендикулярности плоскостей проекций ( П₁ 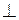П₄ или П₂ 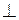П₄)

2) геометрическая фигура по отношению к новой плоскости заняла бы частное положение (параллельное или перпендикулярное)

Причем одновременно можно заменять только одну плоскость проекций.

Рассмотрим пример преобразования чертежа на примере точки.

Пусть в системе плоскостей проекций П₁-П₄ дана точка А (рис. 3). Тогда чертеж этой точки будет выглядеть так, как он задан на рис. 4

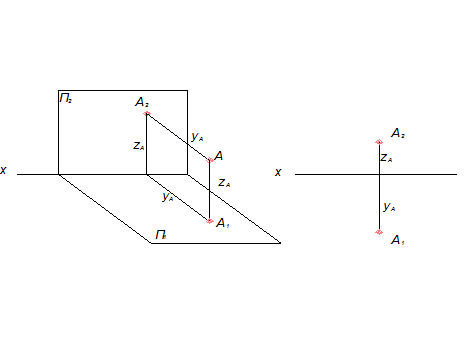
Рис. 3 Рис. 4

Заменим плоскость П₂ на новую П₄, причем П₄ 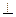П₁, а положение т. А не изменяется (рис.5). спроецируем т. А в системе плоскостей проекций П₁-П₄ и получим новую фронтальную проекцию т. А – А₄

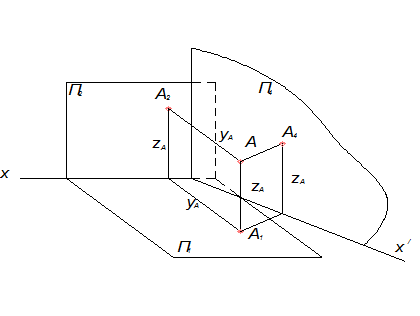
Рис. 5

В результате получим чертеж точки А в системе плоскостей П₁-П₄. Причем при построении чертежа т. А в П₁-П₄ должны соблюдаться следующие положения:

1) линия связи между проекциями А₁ и А₄ перпендикулярна оси проекций X^/ (П₁-П₄)

2) Расстояние от новой фронтальной проекции т. А-А₄ до оси X^/ определяется координатой Z точки А, а следовательно равно расстоянию от А₂ до оси X. (рис. 6)

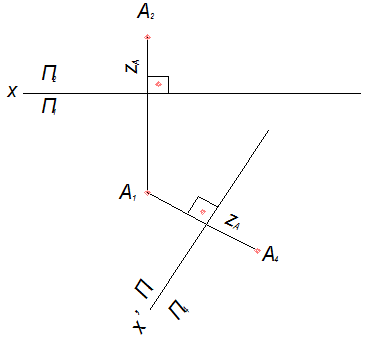
Рис.6

При необходимости можно продолжить преобразование системы плоскостей проекций, заменив плоскость П₁ из системы П₁-П₄ на новую П₅ (П₅ 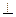П₄). Тогда при этом преобразовании сохранится расстояние от точки А до П₄, а следовательно на чертеже расстояние от А₅ до оси X^// равно расстоянию от А₁ до оси X^/ (рис.7).

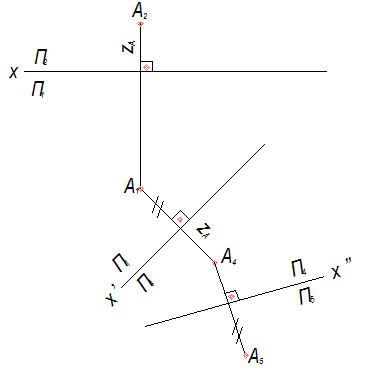
Рис. 7

Метод замены плоскостей проекций прост и удобен для решения метрических задач- задач по определению расстояний между геометрическими фигурами.

Метрические задачи

Все метрические задачи условно можно разбить на две группы:

1) задачи, связанные с прямыми;

2) задачи, связанные с плоскостями