Следует отметить, что процесс разбиения не является однозначным, однако это обстоятельство на конечный результат не влияет.
Второй этап. При рассмотрении второго этапа моделирования представим в рекуррентной операторной и графической формах зависимости между входными и выходными величинами каждого из простейших звеньев, рассмотренных выше. При этом будем пользоваться следующими графическими обозначениями (рис. 13а).
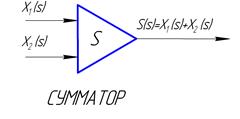
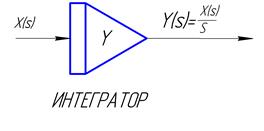
А)
На входах сумматора (интегратора) в кружках могут приостанавливаться коэффициенты, на которые умножается входная величина при суммировании. Например, см.. рис. 13б.
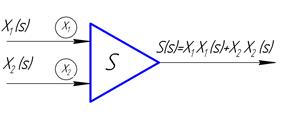
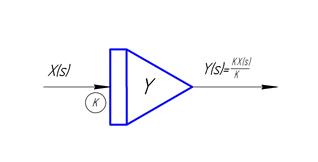
Б)
Рисунок 13. Графические обозначения сумматора и интегратора.
Звено 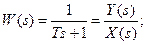
Х(s) – входная величина, а Y(s) – выходная. Разделяем переменные таким образом, чтобы все члены содержание X(s) оказались в левой части уравнения, Y(s) - в правой части (или наоборот);
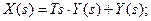 (1)
(1)
Дальнейшее преобразование удобно выполнять в следующей последовательности:
ü отыскиваем член имеющих при Y(s) коэффициент содержащий оператор «s» в максимальной степени;
ü переносим этот член в левую часть, а все остальные в правую;
ü Делим все члены уравнения на коэффициент при выходной величине Y(s), стоящей в правой части, т.е на коэффициент при Y(s) содержащий оператор «s» в максимальной степени. Таким образом, для получения выходной величины Y(s) нам нужно проделать над ленами входящую в правую часть, только операции алгебраического суммирования и интегрирования. Для выражения (1) имеем:
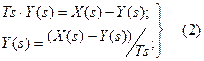
Выражение (2) является рекуррентной операторной формой для расчета динамики звена 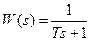 . Графическая форма расчета динамики имеет следующий вид (рис. 14а).
. Графическая форма расчета динамики имеет следующий вид (рис. 14а).
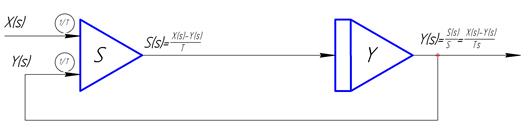
Рисунок 14а. Графическая форма расчета динамики звена 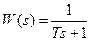 .
.
=================================================
Звено 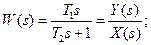
Проделывая в описанном выше порядке преобразования, получаем:
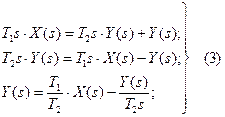
Графическая форма имеет вид (рис. 14б)
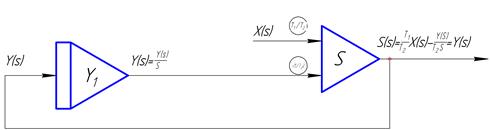
14б. Графическая форма расчета динамики звена 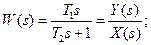
=======================================================
Звено 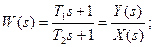
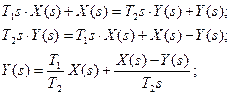
Дата добавления: 2015-11-18; просмотров: 595;
