Производные высших порядков
Производная 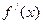 функции
функции 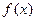 в свою очередь является функцией от х. Ее производная называется производной второго порядка и обозначается
в свою очередь является функцией от х. Ее производная называется производной второго порядка и обозначается 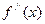 , т.е.
, т.е. 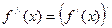 . Другие обозначения
. Другие обозначения
1. 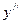 или
или 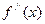 (Лагранж); 3. .
(Лагранж); 3. . 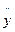 или
или 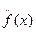 (Ньютон);
(Ньютон);
2. 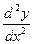 или
или 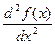 (Лейбниц); 4.
(Лейбниц); 4. 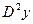 или
или 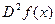 (Коши).
(Коши).
Далее можно искать производную от 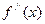 , которую называют производной третьего порядка функции
, которую называют производной третьего порядка функции 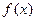 и обозначают
и обозначают 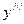 ,
, 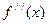 ,
, 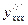 ,
, 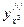 ,
,  и т.д.
и т.д.
Производная от производной п-го порядка называется производной (п+1) -го порядка, 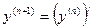 .
.
Пример 1.  .
.
Пример 2. 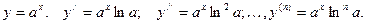
Методом математической индукции можно доказать, что 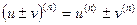 ;
; 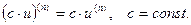
Лекция 3.
Производная параметрически заданной функции
Определение 1. Множество всех точек плоскости, прямоугольные координаты которых представимы как непрерывные на функции переменной t, т.е. , называется параметрически заданной кривой.
Пусть функции 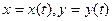 определены в некоторой окрестности точки t0 и одна из них, например x(t), непрерывна и строго монотонна. Тогда в этой окрестности для
определены в некоторой окрестности точки t0 и одна из них, например x(t), непрерывна и строго монотонна. Тогда в этой окрестности для  существует однозначная обратная функция
существует однозначная обратная функция 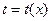 и имеет смысл сложная функция
и имеет смысл сложная функция 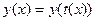 . Эта функция называется параметрически заданной функцией. Она задается системой
. Эта функция называется параметрически заданной функцией. Она задается системой 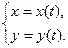
Если 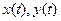 в точке t0 имеют производные и
в точке t0 имеют производные и 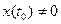 , то параметрически заданная функция у(х) в точке
, то параметрически заданная функция у(х) в точке 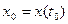 имеет производную
имеет производную 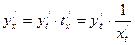 . Т.о.
. Т.о.
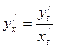 (1)
(1)
Система 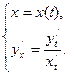 определяет искомую производную в параметрической форме.
определяет искомую производную в параметрической форме.
Пусть существуют 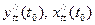 . При нахождении
. При нахождении 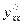 учтем, что
учтем, что 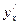 снова параметрически заданная функция, а
снова параметрически заданная функция, а 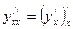 . По формуле (1) имеем
. По формуле (1) имеем 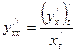 и т.д.
и т.д.
Пример3. 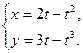
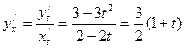 .
. 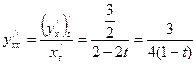 .
.  .
.
Контрольные задания по теме:
Найти производные 1 и 2 порядков
а) 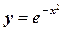 , б)
, б) 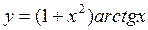 , в)
, в) 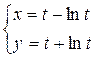 , г)
, г) 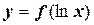 .
.
Дата добавления: 2015-11-18; просмотров: 460;
