Для обратимого цикла Карно справедливо следующее равенство

h_t=1-q₂/q₁=1- T₁₁/T₁, (8.10)

откуда следует:

q₂/q_{1 =} T₁₁/T_{1 ,} q₁/T₁ =q₂/T₂

и S(q/T) =0 (8.11)

Последнее равенство говорит о том, что в обратимом цикле Карно сумма приведённых теплот (q/T) равна нулю.

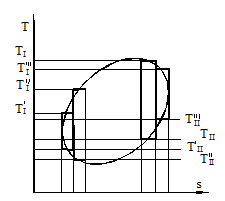
На рисунке 8.5 представлен произвольный обратимый цикл 1234. Для обеспечения необратимости процессов в термодинамической системе должно быть бесконечное множество теплоисточников и теплоприёмников, чтобы на каждом элементарном участке цикла теплообмен происходил при бесконечно малой разности температур. Данный произвольный цикл можно условно разбить на множество элементарных циклов Карно, как это показано на рисунке. Для каждого из этих элементарных циклов S(dq/T) = 0, а для всего цикла при интегрировании

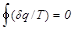(8.13)

Таким образом, для любого обратимого цикла интеграл по замкнутому контуру элементарных приведённых теплот равен нулю.

Для необратимого цикла Карно равенство (8.10) несправедливо, так как термический кпд произвольного цикла меньше, чем у обратимого цикла Карно:

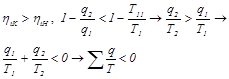(8.14)

В соответствии с выражением (8.14), алгебраическая сумма приведённых теплот для необратимого цикла является отрицательной величиной. В произвольном необратимом цикле, составленном из множества элементарных необратимых циклов Карно при интегрировании по замкнутому контуру получается

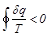(8.15)

Для обратимых и необратимых циклов с учётом (8.13) и (8.15):

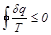(8.16)

Следует учитывать, что входящие в формулы (8.16) и (8.15) величины относятся к рабочему телу, и изменение энтропии, определяемое подынтегральным выражением, характеризует лишь рабочее тело. В термодинамической системе из-за происходящего необратимого преобразования теплоты в работу энтропия всегда увеличивается.