Двухфазная фильтрация несмешивающихся жидкостей.
На вытеснении нефти водой или газом основана технология ее извлечения из недр при разработке месторождений.
Рассмотрим процесс вытеснения, происходящий в прямолинейном тонком горизонтальном образце (Рис. 18), представленной однородной и изотропной средой.
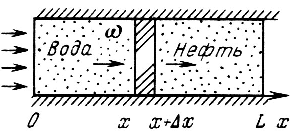 В рассматриваемый образец первоначально заполненный нефтью, через сечение x = 0 закачивается вода.
В рассматриваемый образец первоначально заполненный нефтью, через сечение x = 0 закачивается вода.
Опыты показывают, что расход каждой фазы растет с увеличением насыщенности и градиента давления. Рис. 18. Схема прямолинейно параллельного вытеснения нефти водой.
В этом случае закон фильтрации каждой фазы можно представить в виде обобщенного закона Дарси в дифференциальной форме:
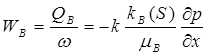 (181)
(181)
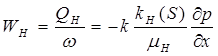 (182)
(182)
Здесь Wв , Qв и Wн , Qн – скорости фильтрации и объемные расходы соответственно воды и нефти, mв, mн – коэффициенты динамической вязкости фаз, kв(S) и kн(S) – относительные фазовые проницаемости, S = Sв – водонасыщенность.
Sв + Sн = 1
Исключим градиент давления 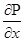 , поделив почленно одно на другое уравнения (181) на (182):
, поделив почленно одно на другое уравнения (181) на (182):
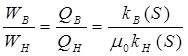 , (183)
, (183)
где 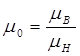 .
.
Применив к (183) правило производных пропорций и использовав соотношения Wв + Wн = W(t) или Qв + Qн = Q(t), (183) получим:
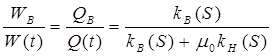
Обозначим
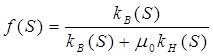 (184)
(184)
Из предыдущего равенства найдем:
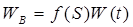 и
и 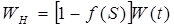 (185)
(185)
Функция насыщенности f(S), называется функцией распределения потоков фаз или функцией Бакли – Леверетта.
Из (175) следует, что f(S), представляющая отношение скорости фильтрации (или расхода) вытесняющей фазы (воды) и суммарной скорости W (или расхода Q), равна объемной доле воды в суммарном потоке двух фаз. Функция f(S) определяет полноту вытеснения и характер насыщенности по пласту. Задача повышения нефти – и газоконденсатоотдачи в значительной степени сводится к применению таких воздействий на пласт, которые, в конечном счете изменяют вид f(S) в направлении увеличения полноты вытеснения.
Из (174) видно, что функция f(S) полностью определяется относительными фазовыми проницаемостями (Рис. 19).
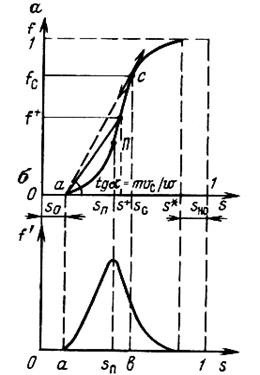 С ростом водонасыщенности f(S) моно
С ростом водонасыщенности f(S) моно
тонно возрастает от 0 до 1. Характерная
особенность графика f(S) – наличие точки
перегиба П с насыщенностью Sп, участков
вогнутости и выпуклости, где вторая про –
изводная f¢¢(S) соответственно больше и
меньше нуля. Эта особенность в большей
степени определяет специфику фильтра –
ционных задач вытеснения в рамках
модели Бакли – Леверетта.
Рис. 19. Зависимость объемной доли вытесняющей фазы (воды) в потоке f(а) и ее производной (б) от насыщенности.
Уравнение
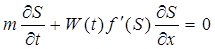 (186)
(186)
Является дифференциальным уравнением только относительно насыщенности. Изменение насыщенности во времени по пласту можно получить в результате решения уравнения (186) независимо от распределения давления р(x, t). Уравнение (186) является уравнением Бакли – Леверетта. Для нахождения распределения насыщенности к уравнению (186) нужно добавить начальное и граничное условия:
При t = 0 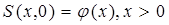
При x = 0 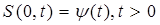 (187)
(187)
Первое из уравнений (187) означает, что в момент времени t = 0 (до начала процесса вытеснения) в пласте имеется некоторое известное распределение насыщенности S вытесняющей фазы, определяемое функцией j(x). Согласно второму условию (187), при t > 0 в пласт через нагнетательную галерею, расположенную на “линии” x = 0, закачивается вытесняющая жидкость (вода), насыщенность которой при x = 0 меняется со временем по заданному закону y(t). В некоторых случаях можно считать, что
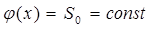
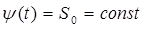 (188)
(188)
Решение уравнения Бакли – Леверетта.
В процессе нагнетания воды в пласт ее насыщенность будет меняться со временем вдоль направления движения x. Связь между S, x и t можно записать в функциональной форме S = S (x, t) или, что эквивалентно, в дифференциальной форме
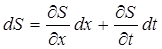 (189)
(189)
Для любого заданного значения можно установить такую связь между x и t, что удовлетворяется уравнение S = S (x, t) = const или эквивалентное дифференциальное уравнение.
Решим совместно два уравнения:
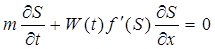
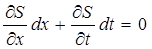 (190)
(190)
Решение системы уравнений (190) дает соотношение между x и t в дифференциальной форме.
Из решения уравнений (190) находим:
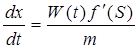 (191)
(191)
Производная dx/dt вычисляется при постоянном значении S, т. е. dx/dt = ¶x/¶t.
Найдем положение х (после интегрирования 191) заданного значения насыщенности как функцию времени:
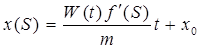 , (192)
, (192)
где хо – значения координат с начальной водонасыщенностью So при t = 0.
Таким образом, уравнения (191) и (192)
dx/dt = w/mf¢(s)
и
x(s) = w/mf¢(s)t + xo
можно использовать для расчета скорости и координаты данного значения насыщенности в области непрерывного профиля, и уравнения
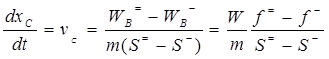 (193)
(193)
индексом “с” обозначены величины, относящиеся к фронту (скачку) насыщенности, а 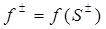 , выражение (193) задает скорость Vc распространения фронта насыщенности и известно как условие на скачке.
, выражение (193) задает скорость Vc распространения фронта насыщенности и известно как условие на скачке.
Равенство (193) имеет простой геометрический смысл: скорость скачка Vc пропорциональная тангенсу угла наклона к оси S секущей, соединяющей точки кривой f(S), имеющие абсциссы с коэффициентом пропорциональности w/m.
Если насыщенности по обе стороны фронта постоянны, уравнение (193) можно проинтегрировать и найти положение фронта как функцию времени:
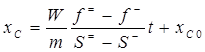 , (194)
, (194)
где хco – положение скачка при t = 0 (хco = 0).
При помощи (193) и (194) можно найти скорость и положение скачка насыщенности.
Приведем простой способ графического построения профиля насыщенности, который состоит в следующем (Рис. 19):
1). В соответствии с данными о фазовых проницаемостях флюидов по формуле (173*) кривая Бакли – Леверетта f(S).
2). Из точки а на кривой f(S), соответствующей начальной водонасыщенности So в пласте, проводится касательная к f(S).
3). Насыщенность в точке касания Sс есть насыщенность, которая устанавливается в пласте непосредственно за фронтом
4). Отрезок на Рис. 19б представляет величину скачка насыщенности Sс – So, которая не меняется со временем (стационарный скачок).
5). Скорость перемещения постоянных насыщенностей, больших Sс, пропорциональна наклону касательной к f(S) в соответствующей точке.
Расчет определения насыщенности
1). Определим насыщенность Sс на скачке (фронтальную насыщенность) из уравнения
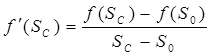 (195)
(195)
При численных расчетах Sс вместо решения уравнения (195) удобно использовать (эквивалентный) способ, не требующий дифференцирования экспериментальной функции f(S). За фронтальную насыщенность следует принять те значения S, которые обеспечивают максимум дроби:
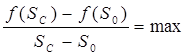 (196)
(196)
Условие (196) означает, что на скачке реализуется то (условие) значение насыщенности, которое обеспечивает ей наибольшую скорость.
2). Зная Sс, из (194) определяют положение хс, скачка насыщенности.
3). По (192) рассчитывают непрерывную ветвь профиля насыщенности при Sс < S < S* и 0 < x < xc.
Дата добавления: 2015-11-10; просмотров: 4100;
