Общая схема исследования функции и построение графика
В предыдущих параграфах было показано, как с помощью производных двух первых порядков изучаются общие свойства функции. Пользуясь результатами этого изучения, можно составить представление о характере функции и, в частности, построить ее график.
Исследование функции 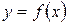 целесообразно проводить по следующей схеме.
целесообразно проводить по следующей схеме.
1. Найти область определения функции.
2. Исследовать функцию на четность и нечетность.
3. Исследовать функцию на периодичность.
4. Найти точки пересечения графика функции с осями координат.
5. Найти интервалы знакопостоянства функции (интервалы, на которых 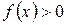 или
или 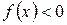 ).
).
6. Найти асимптоты графика функции.
7. Найти интервалы монотонности и точки экстремума функции.
8. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.
9. Построить график функции.
Пример
Исследовать функцию 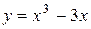 и построить ее график.
и построить ее график.
1. Область определения функции 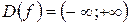 .
.
2. Функция нечетная: 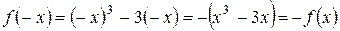 . График функции симметричен относительно начала координат
. График функции симметричен относительно начала координат
3. Функция непериодическая.
4. Точки пересечения с осями координат:
С осью Оу: 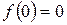 , точка
, точка 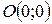 .
.
С осью Ох: 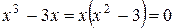 ,
, 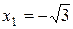 ,
, 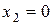 ,
, 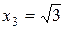 .
.
5. Точки 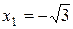 ,
, 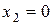 и
и 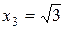 разбивают ось Ох на четыре интервала.
разбивают ось Ох на четыре интервала.
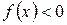 при
при 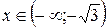 ;
;
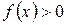 при
при 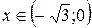 ;
;
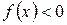 при
при 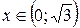 ;
;
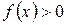 при
при 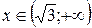 .
.
6. Так как функция является непрерывной, то ее график не имеет вертикальных асимптот.
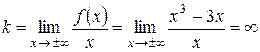 .
.
Наклонной и горизонтальной асимптот нет.
7. 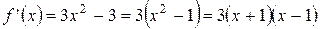 ,
,
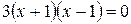 ,
, 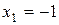 ,
, 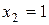 − критические точки.
− критические точки.
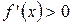 для
для 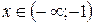 «↑»,
«↑»,
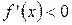 для
для 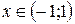 «↓»,
«↓»,
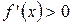 для
для 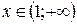 «↑».
«↑».
Сведем данные в таблицу.
| х | 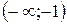
| -1 | 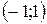
| 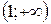
| |
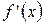
| + | − | + | ||

| ↑ (возрастает) | mах | ↓ (убывает) | min -2 | ↑ (возрастает) |
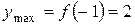 ,
, 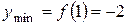 ;
;
точка 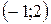 − максимум;
− максимум;
точка 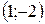 − минимум.
− минимум.
8. 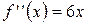 ,
, 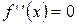 ,
, 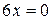 ,
, 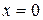 .
.
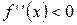 при
при 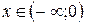 «
« 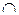 »;
»;
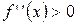 при
при 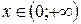 «
« 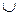 ».
».
| х | 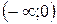
| 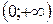
| |
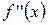
| − | + | |

| 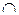 (выпуклый)
(выпуклый)
| (точка перегиба) |  (вогнутый)
(вогнутый)
|
Точка 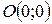 − точка перегиба.
− точка перегиба.
9. График функции 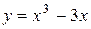 (рис.5.12)
(рис.5.12)
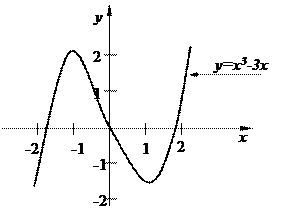 |
Рис. 5.12
Упражнения
Найти интервалы возрастания и убывания функций:
| 1. | 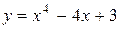 ; ;
| Ответ: 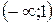 − убывает; − убывает;
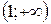 − возрастает. − возрастает.
|
| 2. | 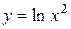 ; ;
| Ответ: 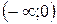 − убывает; − убывает;
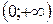 − возрастает. − возрастает.
|
| 3. | 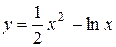 ; ;
| Ответ: 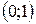 − убывает; − убывает;
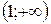 − возрастает. − возрастает.
|
| 4. | 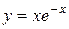 ; ;
| Ответ: 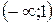 − возрастает; − возрастает;
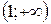 − убывает. − убывает.
|
Найти экстремумы функций:
| 5. | 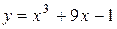 ; ;
| Ответ: нет экстремума. |
| 6. | 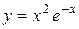 ; ;
| Ответ: 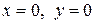 минимум, минимум,
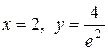 максимум. максимум.
|
| 7. | 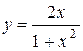 ; ;
| Ответ: 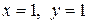 максимум, максимум,
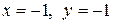 минимум. минимум.
|
Найти наибольшее и наименьшее значения функции на указанных отрезках:
| 8. | 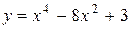 на на 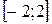 ; ;
| Ответ: 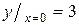 наибольшее, наибольшее,
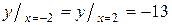 наименьшее. наименьшее.
| |
| 9. | 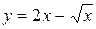 на на 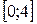
| Ответ: 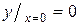 наименьшее, наименьшее,
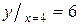 наибольшее. наибольшее.
|
Найти интервалы выпуклости и вогнутости и точки перегиба графиков функций:
| 10. | 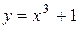
| Ответ: 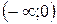 − выпуклость, − выпуклость,
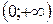 − вогнутость, − вогнутость,
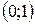 − точка перегиба. − точка перегиба.
|
| 11. | 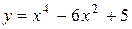
| Ответ: 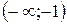 − вогнутость, − вогнутость,
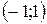 − выпуклость, − выпуклость,
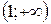 − вогнутость, − вогнутость,
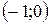 , , 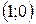 − точки перегиба. − точки перегиба.
|
| 12. | 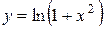
| Ответ: 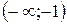 − выпуклость, − выпуклость,
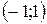 − вогнутость, − вогнутость,
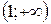 − выпуклость, − выпуклость,
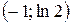 , , 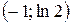 − точки перегиба. − точки перегиба.
|
Найти асимптоты кривых:
| 13. | 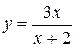
| Ответ: 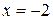 вертикальная; вертикальная;
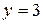 горизонтальная. горизонтальная.
|
| 14. | 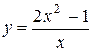
| Ответ: 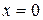 вертикальная; вертикальная;
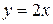 наклонная. наклонная.
|
| 15. | 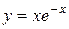
| Ответ: 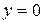 горизонтальная. горизонтальная.
|
Исследовать функции и построить их графики:
| 16. | 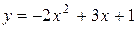
| |
| 17. | 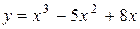
| |
| 18. | 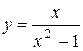
|
Дата добавления: 2015-11-10; просмотров: 710;
