Связь между функцией, ее пределом и бесконечно малой функцией
Сравнивая между собой определения предела функции в точке с определением бесконечно малой функции, можно заметить, что разность между функцией и ее пределом является величиной бесконечно малой.
Утверждение этого факта формулируют в двух теоремах − прямой и обратной.
Теорема (прямая).
Если функция 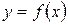 имеет предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции
имеет предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции 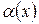 , т.е. если
, т.е. если 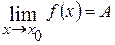 , то
, то
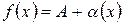 .
.
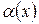 может принимать как положительные, так и отрицательные значения, т.е. функция
может принимать как положительные, так и отрицательные значения, т.е. функция 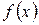 может быть как больше, так и меньше своего предела.
может быть как больше, так и меньше своего предела.
Теорема (обратная).
Если функцию 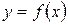 можно представить в виде суммы числа А и бесконечно малой функции
можно представить в виде суммы числа А и бесконечно малой функции 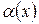 , то число А является пределом функции
, то число А является пределом функции 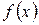 , т.е. если
, т.е. если 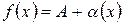 , то
, то
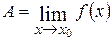 .
.
Основные теоремы о пределах
Приведем без доказательства теоремы, которые облегчают нахождение пределов функций.
Пусть 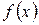 и
и 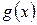 − функции, для которых существуют пределы при
− функции, для которых существуют пределы при 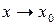 (или
(или 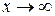 ), т.е.
), т.е. 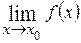 и
и 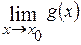 .
.
Теорема.
Если функция 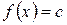 постоянна, то ее предел равен ей самой:
постоянна, то ее предел равен ей самой:
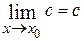 .
.
Теорема.
Предел суммы (разности) двух функций равен сумме (разности) их пределов:
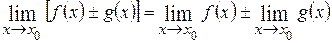 .
.
Следствие.
Функция может иметь только один предел при 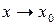 .
.
Теорема.
Предел произведения двух функций равен произведению их пределов:
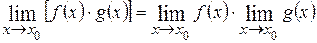 .
.
Следствие.
Постоянный множитель можно выносить за знак предела:
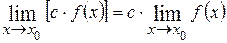 .
.
Следствие.
Предел степени с натуральным показателем равен той же степени предела:
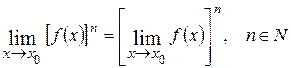 .
.
Теорема.
Если предел функции 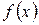 отличен от нуля, то предел обратной ей по величине функции
отличен от нуля, то предел обратной ей по величине функции 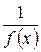 равен обратной величине предела данной функции:
равен обратной величине предела данной функции:
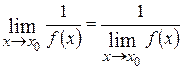 .
.
Теорема.
Предел частного равен частному пределов, если предел знаменателя отличен от нуля:
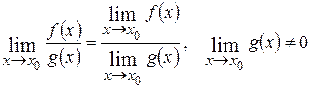 .
.
Теорема.
Если для функции 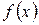 существует
существует 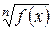 , то
, то
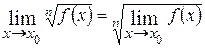 .
.
Дата добавления: 2015-11-10; просмотров: 7943;
