ОБРАЗОВАНИЕ КОНУСА ПОДОШВЕННОЙ ВОДЫ

Рис. 7.11. Схема конуса подошвенной воды

в монолитных пластах, в которых возможно движение жидкости поперек напластований. При создании на скважине определенной депрессии первоначально горизонтальная граница раздела между нефтью и подошвенной водой (водонефтяной контакт) искривляется, образуется водяной холм, который называется конусом.

Точной теории водяного конуса до сего времени не имеется ввиду чрезвычайной сложности задачи. Приближенная теория, позволяющая рассчитать предельный безводный дебит скважины и форму стационарного конуса, была предложена М. Маскетом и И. А. Чарным.

Так как добыча нефти в данном случае сопровождается непрерывным замещением нефти подошвенной водой, конус, вообще говоря, не является стационарным. Однако при достаточно малых депрессиях, характерных для безводного притока нефти, и существенном влиянии силы тяжести образовавшийся конус поднимается медленно и устойчиво. Вертикальные компоненты скорости значительно меньше горизонтальных. Процесс имеет квазистационарный характер. Поэтому для приближенного расчета нестационарного конуса в этих условиях можно применять метод последовательной смены стационарных состояний, при котором конус в каждый момент времени считается стационарным.

Рассмотрим задачу о притоке нефти к несовершенной скважине (по степени вскрытия пласта) при устойчивом неподвижном конусе подошвенной воды. Будем считать пласт изотропным, кровлю и подошву пласта горизонтальными, начальное положение водонефтяного контакта также горизонтальным. Предположим, что водяной конус неподвижен и устойчив и к скважине притекает чистая нефть. Направим оси координат так, как показано на рис. 7.11,а. Обозначим нефтеносную толщину h, глубину вскрытия-b, радиус скважины-r_c.

В точной постановке требуется решить уравнение Лапласа для потенциала 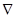²Ф = 0 при следующих граничных условиях: кровля пласта непроницаема; поверхность водонефтяного контакта, форма которой неизвестна и сама подлежит определению, также непроницаема для нефти. Основная сложность такой задачи заключается в том, что форма границы раздела воды и нефти, т.е. форма конуса, неизвестна. Таким образом, помимо трудностей, связанных с решением уравнения Лапласа, неизвестна область, в которой это решение должно быть найдено.

Выясним условия, при которых водяной конус будет неподвижным. Предположим, что распределение давления в любой -точке пласта известно, т.е. известна функция р = p(r, z). Выделим на вершине конуса (r = 0) элементарный вертикальный цилиндрик пористой среды площадью df, высотой dz, заполненный водой, и рассмотрим силы, которые на него действуют (см. рис. 7.11,6), предполагая, что этот цилиндрик попал в нефтяную часть.

Пусть давление на верхнюю грань будет p(0, z)=p, давление на нижнюю грань р'. Очевидно,

.

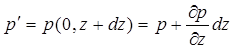Сила, которая влечет эту частицу вверх, равняется

,

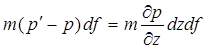где m -пористость.

Вниз частицу воды влечет ее собственный вес, равный ρ_Вgmdzdf, где ρ_В,-плотность воды.

Условие устойчивости частицы воды, таким образом, имеет вид:

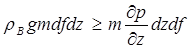или 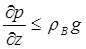. (7.58)

Условие (7.58) можно упростить, перейдя от давления к потенциалу Ф. Для наших условий, когда ось z направлена вниз, имеем:

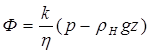, (7.59)

где k –проницаемость; η -вязкость нефти; ρ_н -плотность нефти.

Из формулы (7.59) находим:

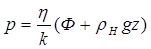, (7.60)

после чего условие устойчивости конуса (7.58) принимает вид

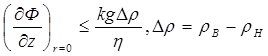. (7.61)

Используем теперь условие, что вода неподвижна и, следовательно. давление в ней распределено гидростатически.

Пусть на некотором расстоянии от скважины R₀ толщина нефтяного пласта равна h₀ и известно давление р₀ на границе раздела. Тогда, так как вода неподвижна, давление в произвольной точке границы раздела:

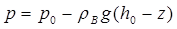(7.62)

Подставив этот значение р в выражение (7.59), получим:

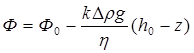, (7.63)

где Фо - потенциал точки с давлением р₀.

Это означает, что вдоль границы раздела текущей нефти и неподвижной воды потенциал изменяется линейно в зависимости от координаты z.

На рис. 7.12 приведены кривые распределения потенциала вдоль оси скважины и вдоль цилиндрической поверхности радиусом R₀. Вдоль поверхности R₀ потенциал будем считать постоянным: Ф = Ф₀ (прямая DN).

Уравнение (7.63) изображается прямой DC, наклоненной к вертикали под углом β, с угловым коэффициентом, равным tg β = k∆ρg/η. Где-то на этой прямой лежит потенциал вершины конуса С. Если бы была известна высота подъема конуса, то сразу можно было бы найти этот потенциал.

Теперь посмотрим, какой вид будет иметь распределение потенциала вдоль стенки скважины и ниже в нефтяной части пласта. Наименьшее давление, а следовательно, и наименьший потенциал будут на стенках скважины, причем вдоль стенок скважины потенциал считается распределенным равномерно, так как на стенке скважины давление можно считать гидростатическим. Обозначим потенциал на стенке скважины Ф_c. Ниже донышка скважины потенциал будет возрастать так, как показано на рис. 7.12, т.е. выпуклостью вправо. Действительно, вертикальная составляющая скорости фильтрации определяется по формуле w_z = - ∂Ф/∂z. Вершина конуса по условию неподвижна. Следовательно, скорость нефти на

Рис. 7.13. Графики для расчета предельных безразмерных дебитов и предельной высоты подъема конуса.

Кривые 1 – 5 - для q(h); 6 – 10 – для hmax; d: 1, 6 –1000; 2, 7 – 100; 3, 8 – 10; 4, 9 – 4; 5, 10 – 1.

что касательная в этой точке должна быть вертикальной. К оси скважины подтекают струйки. Поэтому скорость вдоль оси скважины монотонно возрастает от нуля до максимального значения на донышке. Таким образом, 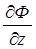, вдоль оси z скважины монотонно возрастает, и кривая распределения потенциала Ф = Ф (0,z) должна быть обращена выпуклостью вправо, как показано на рис. 7.12 (кривая ВС).

Очевидно, высота конуса определяется положением точки пересечения С прямой DC и кривой Ф = Ф (0, z).

Предположим теперь, что при сохранении потенциала Ф0 дебит скважины начал увеличиваться. Это достигается соответствующим уменьшением забойного потенциала Фc на стенке скважины. Условие устойчивости водяного конуса выражается формулой (7.61).

Отсюда следует, что перед началом прорыва воды распределение потенциала в нефтяной части Ф (0,z) ниже дна скважины будет изображаться кривой С' В', касательная к которой в вершине конуса составит c вертикалью угол 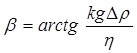. Дебит скважины 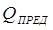, соответствующий предельному состоянию конуса, называется предельным безводным дебитом.

Однако точный вид распределения потенциала при наличии конуса обводнения неизвестен. Поэтому нужно исходить из каких-то других предпосылок, которые позволят оценить приближенно величину подъема конуса и наиболее интересную для практики величину - предельного безводного дебита.

Теория конусообразования Маскета-Чарного исходит из допущения, что стеснение потока нефти образующимся водяным конусом мало влияет на распределение потенциала в нефтяной части пласта, и поэтому для приближенной оценки предельных значений дебита и высоты подъема конуса можно воспользоваться известным выражением для потенциала напорного (невозмущенного) течения нефти в однофазно-анизотропном пласте с горизонтальной проницаемостью kr и вертикальной проницаемостью kz .

Анализируя распределение потенциала вдоль оси скважины при невозмущенном и возмущенном движении нефти, И. А. Чарный установил верхний и нижний пределы, между которыми находится предельный безводный дебит:

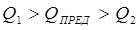. (7.64)

При этом верхний предел Q1 находится в результате сопоставления движения нефти при наличии конуса воды с плоскорадиальным стационарным напорным потоком нефти в пласте с постоянной толщиной h0 , нижний предел Q2 определяется из решения задачи о напорном притоке нефти к несовершенной скважине в пласте толщиной h0 (см. § 6 гл. 3).

Расчеты показывают, что Q1 и Q2 различаются на 25-30%, причем 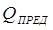ближе к Q1, чем к Q2 .

Результаты расчетов приведены в виде графиков зависимости предельных безразмерных дебитов 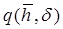и предельной высоты подъема конуса 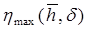на рис. 7.13, где введены безразмерные переменные и параметры:

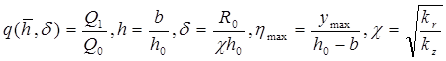
Здесь 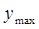- предельная высота подъема конуса перед прорывом;

.

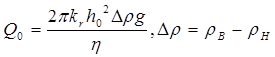Все сказанное, очевидно, полностью распространяется на случай прорыва верхнего газа при наличии газовой шапки. Под Dr при этом следует понимать разность плотностей нефти и газа. Приведенные графики можно также использовать для расчетов в пластовых условиях, предельных безводных дебитов несовершенных газовых скважин в пластах с подошвенной водой.

Расчеты показывают, что безводный дебит в однородных маломощных пластах очень мал. Однако на практике скважины дают иногда довольно большой нефтяной дебит без воды, хотя известно, что под ними имеется подошвенная вода. Это объясняется наличием непроницаемых или малопроницаемых пропластков, которые затрудняют вертикальное движение воды.

Обширный цикл экспериментальных, доследовании, связанных с конусообразованием, выполнен Д. А. Эфрехгом и его сотрудниками на щеле-вых моделях. В результате этих исследований было подтверждено неравенство (7.64) для предельного безводного дебита. Экспериментальное исследование нестационарного газового конуса на физической модели проведено А.К.Курбановым.