Прямолинейно-параллельный неустановившийся
фильтрационный поток упругой жидкости
Случай 1. В момент времени t = 0 в горизонтальном пласте постоянной толщины h и ширины В пущена в эксплуатацию прямолинейная галерея с постоянным дебитом Q. До Пуска галереи давление во всем пласте было одинаковым и равным рк.
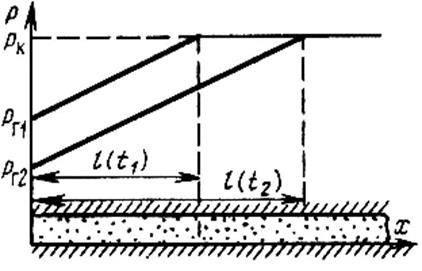
К моменту времени t после пуска галереи граница возмущенной области распространится на длину l(t) (рис. 5.8). Распределение давления в этой области считается установившимся (см. гл. 3, § 2), т.е. имеет линейный характер:
 |
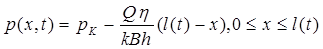 , (5.75)
, (5.75)
Рис. 5.8. Кривые распределения давления в прямолинейно-параллельном потоке по методу ПССС
Требуется найти закон перемещения во времени внешней границы возмущенной области l(t).
Воспользуемся соотношением (5.7), которое состоит в том, что количество добытой продукции за время dt равно изменению упругого запаса жидкости в возмущенной зоне пласта за тот же промежуток времени:
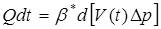 , (5.76)
, (5.76)
где V(t) -объем возмущенной зоны пласта,
V(t) = В hl(t); (5.77)
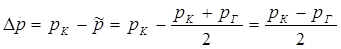 . (5.78)
. (5.78)
Приняв во внимание, что р(х, t) = pг(t) при х = 0, из (5.75) найдем:
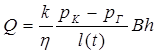 . (5.79)
. (5.79)
Подставив равенства (5.77)-(5.79) в соотношение (5.76), получим:
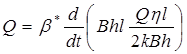
или
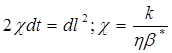 ,
,
откуда после интегрирования найдем:
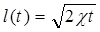 (5.80)
(5.80)
Тогда распределение давления в пласте (5.75) будет иметь следующий вид:
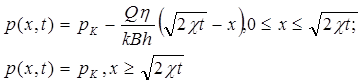 (5.81)
(5.81)
Значения депрессии рк — рг по приближенной формуле (5.81) значи-
тельно отличаются от данных расчетов по точной формуле (5.48): погрешность, составляет 25%.
Случай 2. В таком же пласте, как ив случае 1, в момент времени t = 0 пущена эксплуатационая галерея с постоянным забойным давлением рг = =const. Требуется найти распределение давления, закон перемещения границы возмущенной области l(t) и изменение дебита галереи во времени Q(t).
Дебит галереи в условиях установившегося движения, очевидно. можно выразить следующим образом:
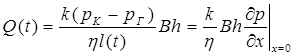 .
.
Задача решается аналогично предыдущему случаю. В результате
находим:
закон движения границы возмущенной области
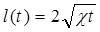 ,
,
распределение давления в возмущенной зоне пласта
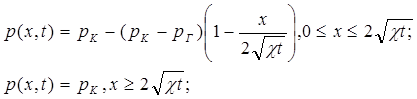 (5.82)
(5.82)
дебит галереи
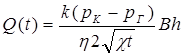 . (5.83)
. (5.83)
Погрешность расчета дебита галереи по приближенной формуле (5,83), по сравнению с расчетами по точной формуле (5.39) составляет 11%.
Следовательно, методом последовательной смены стационарных состояний лучше пользоваться в случае неустановившихся прямолинейно-параллельных потоков при заданной постоянной депрессии.
Плоскорадиальный неустановившийся фильтрационный поток упругой жидкости
Случай 1. Пусть в неограниченном горизонтальном пласте постоянной толщины h в момент времени t = 0 пущена добывающая скважина радиусом rc с постоянным дебитом Q. До пуска скважины давление во всем пласте было одинаковым и равным pк.
В соответствии с методом ПССС принимаем, что через время t после пуска скважины вокруг нее образуется возмущенная область радиусом R(t), где давление будет распределяться по стационарному закону:
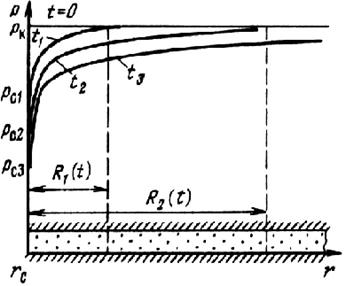 |
Рис. 5.9. Кривые распределения давления в плоскорадиальном потоке в разные моменты времени по методу ПССС (отбор осуществляется при условии Q = const)
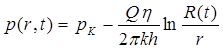 . (5.84)
. (5.84)
В остальной части пласта сохраняется начальное пластовое давление рк.
Требуется найти закон движения границы возмущенной области R(t). Кривые распределения давления в разные моменты времени в таком потоке приведены на рис. 5.9. Дебит скважины, очевидно, будет описываться формулой, аналогичной формуле Дюпюи:
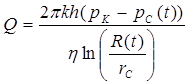 (5.85)
(5.85)
Размеры возмущенной области найдем из уравнения материального баланса (5.76) при
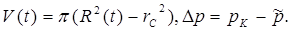 (5.86)
(5.86)
Средневзвешенное пластовое давление 
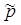 , в установившемся плоскорадиальном потоке (см. гл. 3, § 3, п. В):
, в установившемся плоскорадиальном потоке (см. гл. 3, § 3, п. В):
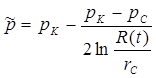 ,
,
откуда, учитывая (5.85), находим:
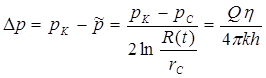 , (5.87)
, (5.87)
Закон движения границы возмущенной области R(t) найдем, подставив выражения (5.86) и (5.87) в уравнение материального баланса (5.76):
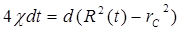 ,
,
откуда после интегрирования в пределах от 0 до t и от rc; до R(t), найдем:
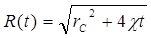 . (5.88)
. (5.88)
Тогда из равенства (5.84) можно определить давление в любой точке пласта в момент времени t:
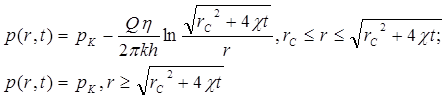 (5.89)
(5.89)
Депрессия в момент времени t:
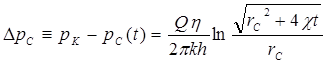 . (5.90)
. (5.90)
Сравнивая (5.90) с депрессией, определенной по точной формуле (5.62), можно убедиться, что относительная погрешность уменьшается с течением времени и составляет 10,6%, если fо = 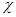 t/r
t/r 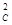 = 100; 7,5%, если (fо = 103; 5,7%, если fo = 104.
= 100; 7,5%, если (fо = 103; 5,7%, если fo = 104.
Случай 2. В случае плоскорадиального потока жидкости к скважине, пущенной в эксплуатацию с постоянным забойным давлением рc = const. закон движения границы возмущенной области выражается интегралом, представляемым в виде медленно сходящегося ряда, поэтому решение здесь не приводится.
Расчет движения границы возмущенной области в этом случае можно определить по графику (рис. 5.10).
Дебит скважины определяется по формуле Дюпюи (5.85) при
Рc = const.
Сравнение с точными расчетами, выполненными К. А. Царевичем и И.Ф. Курановым, показывает, что погрешность определения дебита по методу ПССС составляет около 5%.
Заметим, что как в случае линейной, так и радиальной фильтрации в точке перехода от возмущенной к невозмущенной области градиент давления претерпевает разрыв, что служит одной из причин расхождения
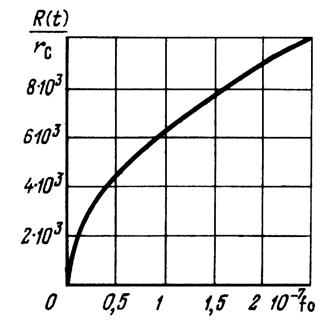
Рис. 5.10. Зависимость безразмерного радиуса возмущенной области R(t)/rc от безразмерного времени fo при отборе жидкости с постоянным забойным давлением рc = const
между результатами расчетов по методу ПССС и точным решением. Однако этот метод служит достаточно эффективным расчетным приемом, позволяющим найти решение в простом виде, чем и объясняется его применение в некоторых случаях не только для задач фильтрации однофазного флюида, но и для задач о движении газированной жидкости и о перемещении границы раздела жидкостей и газов.
Распределение давления в области фильтрации, получаемое по методу ПССС, является довольно грубым приближением; гораздо точнее этим методом дается связь между дебитом и депрессией, особенно в случае радиальной фильтрации.
Дата добавления: 2015-11-10; просмотров: 1561;
