Основные параметры кодов

Рассмотрим наиболее важные параметры, характеризующие линейные коды, на основании которых можно осуществить их выбор и сравнение.

Избыточность:

Абсолютная избыточность

r = n - m

где n – число разрешенных уровней выходного сигнала; m – число разрешенных уровней входного сигнала.

Относительная избыточность

R = r/n = 1 – m/n.

В случае, когда используется двоичный двухуровневый код, n = m = 2 и избыточность блочного кода = 0.

Избыточность придает сигналу заданные свойства и повышает тактовую частоту

f_тл = (n/m)f_т ,

f_т – тактовая частота информационного цифрового сигнала на входе кодера линейного тракта (или на выходе декодера); f_т.л – тактовая частота информационного цифрового сигнала на выходе кодера линейного тракта (или на входе декодера линейного тракта), то есть в линии передачи.

Но при достаточно больших m и незначительной разности m – n это увеличение незначительно.

Относительная скорость передачи (коэффициент изменения тактовой частоты, эффективность кода)

.

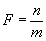Этот параметр характеризует увеличение скорости передачи (увеличение тактовой частоты) при применении данного блочного кода. Очевидно, что чем меньше избыточность кода, тем меньше разница между скоростями.

Максимальное число следующих друг за другом одинаковых по амплитуде (уровню) символов. Для бинарных кодов это максимальное число последовательных "нулей" и "единиц", которое может иметь линейный сигнал. Эти параметры желательно выбирать минимальными, чтобы упростить тракт выделения тактовой частоты.

Среднее значение символов (b_k). Если вероятность появления нулей и единиц в информационном сигнале одинакова (P₀ =P₁=0,5), то (b_k) = 0,5. Для уменьшения средней оптической мощности излучателя и дробового шума фотодетектора среднее значение символов целесообразно выбирать минимальным.

Цифровая сумма (ЦС). Цифровой суммой называют алгебраическую сумму амплитуд импульсов на временном отрезке n-уровневого кода, отнесенную к абсолютному значению разности соседних по величине уровней. Различают цифровую сумму двух видов: накопленную цифровую сумму (НЦС) кодового блока, кодовой группы, кодового слова и текущую цифровую сумму (ТЦС).

Накопленная цифровая сумма – это число возможных значений, которое принимает цифровая сумма для одного блока кода; накопленная цифровая сумма блока из n элементов двухуровневого сигнала

.

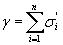Для двоичных кодов значения элементов σ_i цифровой суммы определяются вероятностями появления единиц (P_1л) и нулей (P_0л = 1 – P_1л); σ_i = P_0л для символов "1"; σ_i = - P_1л для символов "0". Накопленная цифровая сумма совпадает с числом состояний кодека (кодера-декодера), и ее величина определяет сложность кодека.

Текущая цифровая сумма определяется алгебраической суммой амплитуд n-уровневого кода с любого момента времени до момента наблюдения

,

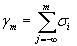где j – порядковый номер бита кодовой комбинации кода в начале отсчета времени; m – порядковый номер бита в момент наблюдения.

Число возможных состояний текущей цифровой суммы в моменты окончания кодовых блоков обозначается S_k. Увеличение S_k приводит к увеличению сложности кодека.

Одновременно усложняется контроль блочной синхронизации. Кроме того, для любого кода существует определенное число значений, обозначенное S_m, которое может иметь текущая цифровая сумма при безошибочном приеме элементов кода. Сложность схемы контроля ошибок определяется S_m.

Плотность непрерывной составляющей спектра в области низких частот, примыкающих к частоте f = 0. Она оценивается коэффициентами Δ₁ и Δ₂ (доли мощности непрерывной составляющей энергетического спектра сигнала, сосредоточенные в области частот от нуля до нуль целых три сотых и от нуля до нуль целых одна десятая соответственно). При отсутствии или низком уровне непрерывных составляющих в низкочастотной части энергетического спектра кода кроме отмеченных выше достоинств имеется возможность эффективно передавать сигналы служебной связи и телеконтроля, а также уменьшать межсимвольные искажения второго рода.

Величина непрерывной составляющей на фиксированной частоте. Эта величина представляет интерес в зависимости от того, какая дискретная составляющая выделяется для системы синхронизации.

Ширина полосы ΔF, содержащая девяносто процентов энергии элементарного импульса линейного кода. Этот параметр характеризует удельную часть непрерывной части энергетического спектра на тактовом интервале Т.

Эффективностьлинейного кода по энергетическим затратам. Этот параметр характеризует энергетические затраты оптических передатчиков при выбранном коде и потери мощности за счет отклонения от оптимальной формы оптического сигнала. С этой точки зрения достоинствами выбранного кода являются экономия мощности и увеличение ресурса лазера.

Коэффициент относительной помехоустойчивости. Он показывает, на какую величину потенциальная помехоустойчивость цифрового сигнала отличается от предельной помехоустойчивости:

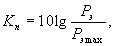
где P_э – эквивалентная потенциальная помехоустойчивость рассматриваемого кода; P_{э max} – предельная эквивалентная потенциальная помехоустойчивость цифрового сигнала.

Вне зависимости от конкретных условий реализации линейного тракта ВОСП сравнение цифровых сигналов удобно производить по потенциальной помехоустойчивости при идеальных условиях, которая зависит от эквивалентной мощности P_э элементов этого сигнала S_i (t) и S_j (t), то есть

.

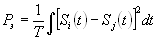Очевидно, что предельной помехоустойчивостью будут обладать сигналы, элементы которых противоположны и удовлетворяют равенству

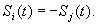
В оптических системах передачи противоположными являются сигналы, которые состоят из элементов высокого (положительного) уровня S_i (t) и низкого (нулевого) уровня S_j (t). Также учтем факт, что при оптимальном приеме достоверность приема тем выше, чем больше энергия сигнала.