Анализ алгоритмов

3.1 Быстродействие – основной показатель эффективности алгоритма

Анализ алгоритмов заключается в том, чтобы предсказать требуемые для его выполнения ресурсы. Иногда оценивается потребность в таких ресурсах, как объем памяти, пропускная способность сети или необходимое аппаратное обеспечение, однако чаще всего определяется время вычислений.

Если бы компьютеры были неограниченно быстрыми, подошел бы любой корректный алгоритм решения задачи. Сегодня есть весьма производительные компьютеры, но их быстродействие не может быть бесконечно большим. Память тоже дешевеет, но она не может быть бесплатной. Следовательно, время вычислений – это такой же ограниченный ресурс, как и объем необходимой памяти. Разумному распределению этих ресурсов способствует применение алгоритмов, эффективных с точки зрения расходов памяти и времени. При этом решающим фактором выбора алгоритма является время его выполнения.

Время работы алгоритма зависит от аппаратного обеспечения (процессора, тактовой частоты, размера памяти, объема дискового пространства и т.п.) и программного обеспечения (операционной системы, среды программирования, компилятора), с помощью которых осуществляется реализация, компиляция и выполнение алгоритма. Например, при всех равных условиях время выполнения алгоритма для определенного количества исходных данных будет меньше при использовании более мощного компьютера или при записи алгоритма на машинном коде по сравнению с его исполнением машиной, которая выполняет интерпретацию текста алгоритма. Однако решающим фактором, влияющим на быстродействие, считается размер входных данных алгоритма.

Очевидно, время выполнения алгоритма возрастает при увеличении размера исходных данных (input size). Например, время, затрачиваемое на сортировку числового массива, увеличивается при увеличении количества сортируемых чисел. Для сравнительного анализа нескольких алгоритмов, решающих одну и ту же задачу, целесообразно применить следующую методику:

1) задать для эксперимента один из сравниваемых алгоритмов;

2) для заданного алгоритма провести ряд экспериментов, в которых используется различное количество исходных данных N ( );

3) далее полученные результаты наглядно представляются в виде графика, на котором каждый m-й случай (m = 1, 2, …, M) выполнения алгоритма обозначается с помощью одиночной точки. У этой точки координата по оси абсцисс равна размеру исходных данных , а координата по оси ординат – времени выполнения алгоритма ;

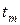4) задать следующий проверяемый алгоритм, и если он не является последним в наборе алгоритмов, то перейти к п. 2, если набор сравниваемых алгоритмов исчерпан, то завершить анализ.

Результатом применения такой методики является диаграмма с графиками, число которых равно количеству исследуемых алгоритмов. На рисунке 3.1 показан случай, когда сравниваются два алгоритма.

Рисунок 3.1 – Результаты исследования времени выполнения двух алгоритмов

Результаты, представленные на рисунке 3.1, показывают, что график времени выполнения алгоритма 2 располагается ниже графика для алгоритма 1. Следовательно, алгоритм 2 является более эффективным, нежели алгоритм 1, для заданных наборов исходных данных.

Чтобы сделать более определенные выводы на основе экспериментальных исследований, необходимо использовать не одиночные, а многочисленные корректные экземпляры исходных данных для достаточно большого числа экспериментов. Это позволит определить некоторые статистические характеристики в отношении времени выполнения алгоритмов.

Экспериментальные исследования очень полезны, однако при их проведении существуют три основных ограничения:

- эксперименты могут проводиться с использованием ограниченного числа наборов исходных данных;

- для сравнения эффективности двух алгоритмов необходимо, чтобы эксперименты проводились на одинаковом аппаратном и программном обеспечении;

- для экспериментального изучения необходимо провести реализацию и выполнение алгоритма.

Чтобы провести анализ алгоритма без экспериментов, можно использовать аналитический подход, который заключается в подсчете простейших операций, выполняемых при работе алгоритма.