Упражнения. 1. На языке последовательностей и языке “e – d” сформулировать определения б.б

1. На языке последовательностей и языке “e – d” сформулировать определения б.б. функций при 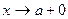и a – 0 ( 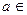R), а также при x→ +∞, –¥ и ¥.

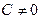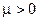2. Пусть а, C и m – вещественные числа, где , а , и пусть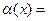 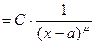. Доказать, что 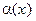является б.б. функцией при 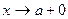; если же m > 0 таково, что a определена и при x < a (например, m Î N), то 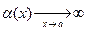Указание, Использовать теорему 1 и пример 2 из п. 4.6. .

3. Пусть C и m – вещественные числа, где 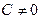и 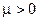, и пусть 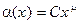. Доказать, что a является б.б. функцией при 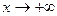; если же 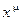определена и при x < 0, то 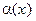является б.б. функцией 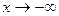при и при .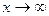

4. Доказать утверждения, аналогичные утверждениям а) – г) из п.3.7.: пусть функции f и g определены в 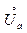, a Î R; тогда

а) если 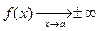, , 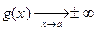то 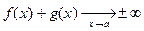(здесь следует выбирать либо везде знак “+”, либо везде знак “–”);

б) если 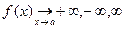, а функция g ограничена в 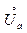(в частноcти имеет конечный предел при x ® а ), то f (x) + g (x) ® +¥, –¥, ¥ соответственно;

в) если 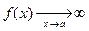, , 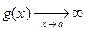то ;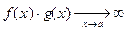

г) если 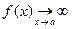, , 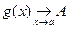где A Î R, A ¹ 0, то .

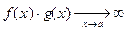5. Сформулировать и доказать утверждения, аналогичные утверждениям а) - г) для функций, бесконечно больших при x ® a + 0, a – 0, где a Î R, а также при x ® +¥, –¥, ¥.