Структурный синтез цифрового автомата по графу

Табличный и графический способы задания автоматов эквивалентны, поэтому граф автомата содержит всю необходимую информацию о функциях выходов и функциях переходов. На граф кодированного цифрового автомата следует нанести все необходимые данные по функциям возбуждения триггеров заданного типа. Однако дальнейшее использование информации, заданной в виде разметки графа цифрового автомата, выполняется с использованием табличного или аналитического представления ФАЛ. Таким образом, синтез цифрового автомата только по графу обычно не делается и этот метод синтеза цифрового автомата является гораздо менее распространённым, чем синтез цифрового автомата с использованием таблиц. На рис.58 представлен пример различных видов разметки графа цифрового автомата Мили S₁₈.

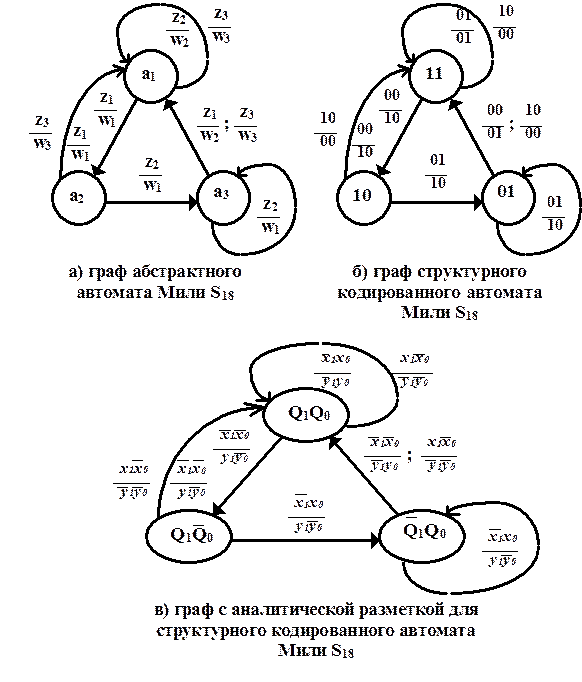
Рис.58 Различные виды разметки графа автомата Мили S₁₈

Функцию выходов по графу рис.58в) получим следующим образом:

- для каждой дуги графа, выходящей из вершины и помеченной выходным сигналом y_i, образуем конъюнкцию из членов, обозначающих эту вершину, и входного сигнала, обеспечивающего движение по этой дуге (то есть выполним конкатенацию этих элементов). Дизъюнкция построенных конъюнкций (конкатенаций) и даёт булеву функцию выхода y_i. Вершины обходятся последовательно, начиная с начальной.

Несколько сложнее обстоит дело с получением функций возбуждения триггеров блока памяти. Функции возбуждения получаются по разметке дуг графа синтезируемого цифрового автомата, которая производится с использованием матриц (таблиц) переходов для заданного типа триггеров в блоке памяти.

Триггеры типа RS. Пример разметки дуг фрагмента графа автомата приведён на рис.59.

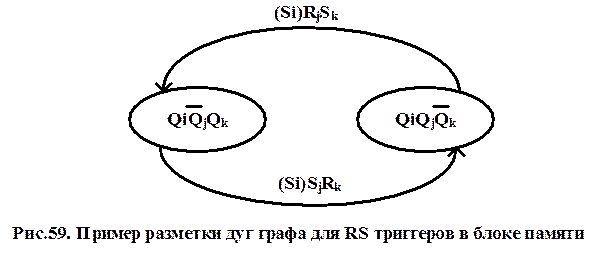
При разметке переходы триггера 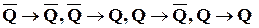интерпретируются как переходы 0®0, 0®1, 1®0, 1®1 соответственно. Если на каком-то из переходов функция возбуждения имеет единичное значение, то дуга графа помечается символом этой функции с соответствующим индексом. Если же на каком-то из переходов функция возбуждения не определена, то дуга помечается символом функции возбуждения заключённым в скобки и имеющим соответствующий индекс.

Триггеры типа T. На рис.60 приведён пример разметки дуг фрагмента графа цифрового автомата для Т триггеров в блоке памяти.

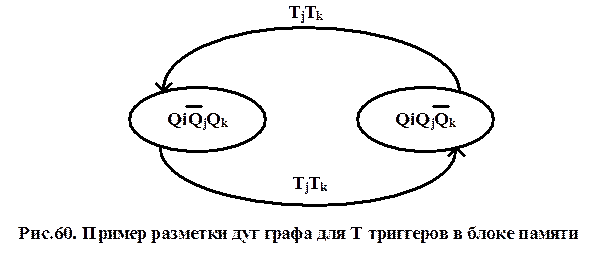
Триггеры типа D. На рис.61 приведён пример разметки дуг фрагмента графа цифрового автомата для D триггеров в блоке памяти.

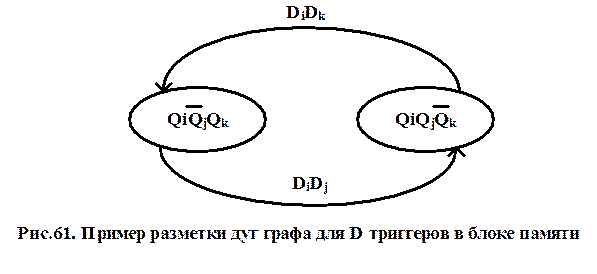Триггеры типа JK. На рис.62 приведён пример разметки дуг фрагмента графа цифрового автомата для JK триггеров в блоке памяти.

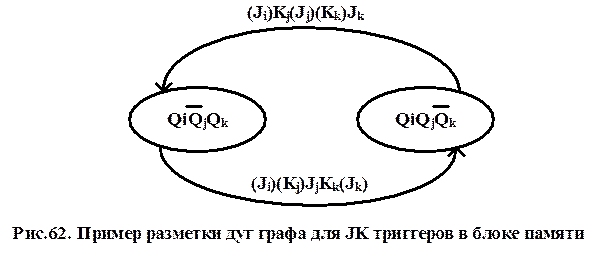
Для каждой помеченной дуги образуется конкатенация кода состояния, из которого выходит дуга, и кода входного сигнала, вызвавшего переход по этой дуге. Соответствующие конъюнкции объединяются в дизъюнкцию и, таким образом, получаются функции возбуждения триггеров блока памяти цифрового автомата. В случае необходимости эти функции подвергаются минимизации любым из ранее рассмотренных способов.

Для структурного синтеза цифровых автоматов предпочтительнее использовать табличные методы, поскольку они выполняются в более жёсткой форме, чем структурный синтез по графу, который требует глубокого сосредоточения внимания на процедуре синтеза и проверке её результатов. Количество ошибок при использовании метода структурного синтеза по графу превосходит количество ошибок при использовании табличного метода структурного синтеза при равных прочих условиях выполнения процедур синтеза.

Несмотря на обоснованное утверждение о равноценности двух рассмотренных методов структурного синтеза, в учебной литературе обычно используется структурный синтез цифровых автоматов по таблицам. В учебных заданиях студенты приобретают навыки выполнения структурного синтеза цифровых автоматов по таблицам и в дальнейшем, в случае необходимости, используют его и в практической инженерной работе.

Заключение

В рассмотренном выше учебно-методическом пособии теория цифровых автоматов рассмотрена с позиции оценки её практической ценности. Как раздел теории цифровых автоматов без памяти (теории булевых функций), так и раздел теории цифровых автоматов с памятью содержат множество примеров, показывающих, что цикл проектирования цифровых автоматов, от составления описания до получения принципиальной схемы, имеет минимальную длительность и малое количество этапов проектирования. По этому показателю теория цифровых автоматов вообще превосходит любую другую теорию. Основная перспектива развития и практического применения теории цифровых автоматов лежит в области автоматизации проектирования сложных схем цифровых автоматов с помощью программ для цифровых вычислительных машин.

ЛИТЕРАТУРА

1. Савельев А.Я. Прикладная теория цифровых автоматов. -М.: Высшая школа, 1987.

2. Баранов С.И., Скляров В.А. Цифровые устройства на программируемых БИС с матричной структурой. -М.: Радио и Связь, 1986.

3. Щелкунов Н.Н., Дианов А.П. Процедуры программирования логических матриц, - Микропроцессорные средства и системы, 1986, №2.

4. Иванов В.И. Синтез цифровых автоматов для систем связи и управления.

Челябинск, ЧПИ, 1980.

5. Баранов С.И. Синтез микропрограммных автоматов. - Л.: Энергия, 1979.

ТЕОРИЯ КОНЕЧНЫХ АВТОМАТОВ

Учебное пособие

Техн. редактор

Издательство Южно-Уральского государственного университета

Подписано в печать 26.02.2014. Формат 60´84 1/16. Печать офсетная.
Усл. печ. л. 4,5. Уч.-изд. л. 4,5. Тираж 100 экз. Заказ 276.