Доведення.

І спосіб. Покажемо, що функція 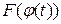є первісною для функції 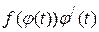. Для цього обчислимо похідну від 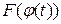як від складної функції:

.

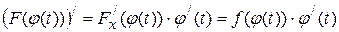(19.20)

Наведемо низку тотожних перетворень, через яку можна перейти від невизначеного інтеграла у правій частині рівності (19.19) до невизначеного інтеграла у її лівій частині:

.

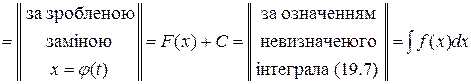ІІ спосіб.Якщо від функції 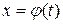, крім неперервності разом із своєю похідною, вимагати ще існування оберненої функції 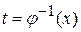, тоді можна запропонувати інший спосіб доведення теореми.

За правилом диференціювання оберненої функції:

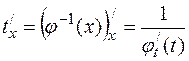або у інших позначеннях .

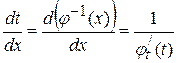Звідки маємо

.

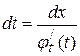(19.21)

Виконаємо перетворення підінтегрального виразу у інтегралі :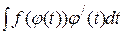

.

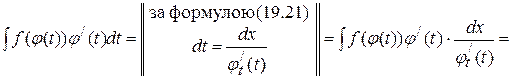
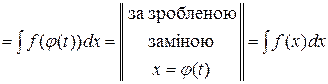(19.22)

Таким чином, ми показали (перетворення (19.22)) як від правої частини формули (19.19) перейти до її лівої частини. Теорема доведена.

Приклад 19.2. Обчислити невизначений інтеграл .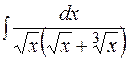

Запропонований приклад є ілюстрацією першого випадку інтегралів, для яких доцільною є заміна виду 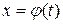, а саме 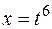. У загальному випадку ця заміна буде розглядатися пізніше у темі: "Інтегрування ірраціональних функцій". Доцільність підстановки обґрунтовується можливістю після її застосування скористатися формулою табличного інтегрування для обчислення заданого інтеграла.

.

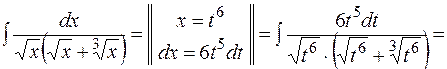
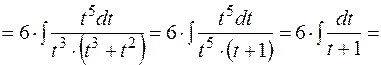
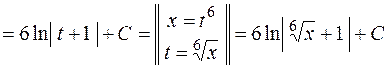Наступна серія прикладів стосується другого випадку застосування методу заміни змінної. Треба зауважити, що застосування методу заміни змінної є певною мірою мистецтвом, яке ґрунтується на доброму знанні правил диференціювання та наполегливості у набутті досвіду аналізу структури підінтегральної функції. Для полегшення процесу набуття такого досвіду розглянемо низку прикладів, на підставі розв’язання яких сформулюємо практичні правила вибору доцільної заміни.

Приклад 19.3. Обчислити невизначені інтеграли:

1) 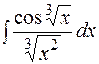;	2) ;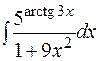
3) 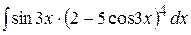;	4) ;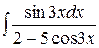
5) 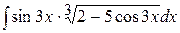;	6) ;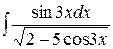
7) 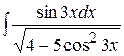;	8) .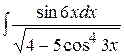

Розв’язання.

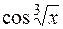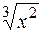1) Підінтегральна функція є часткою двох функцій: і . Більш складною є функція . Похідна від її аргументу з точністю до постійного множника дорівнює простішій частині підінтегральної функції: 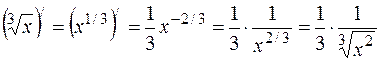. Тому доцільно новою змінною позначити аргумент функції косинус:

.

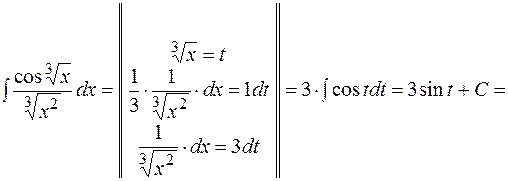
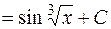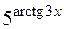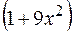2) Підінтегральна функція є часткою двох функцій: і . Більш складною є функція 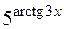. Похідна від її аргументу з точністю до постійного множника дорівнює простішій частині підінтегральної функції: 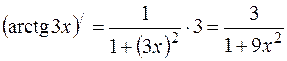. Тому доцільно новою змінною позначити аргумент показникової функції:

.

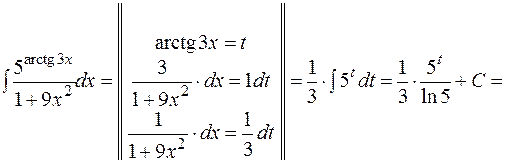
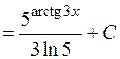3) Підінтегральна функція складається із двох множників: одного більш простої структури 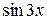та другого – більш складної структури 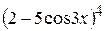. Причому похідна від виразу 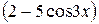з точністю до постійного множника співпадає з більш простим множником. Ці спостереження повинні привести до думки про доцільність заміни 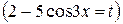. Тобто за нову змінну позначаємо вираз, що є лінійним відносно функції 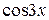. На другому кроці введення нової змінної обчислюють диференціали від обох частин рівності: 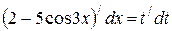. Звідки отримують, що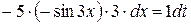 . 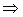Таким чином, обчислення заданого невизначеного інтеграла зводиться до наступних дій:

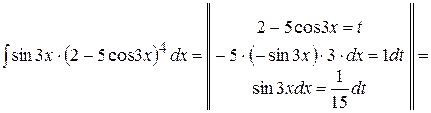
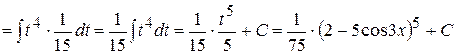
4) Підінтегральна функція має таку саму структуру як і в першому інтегралі, тому скористаємося тією самою заміною, але після підстановки отримаємо інший табличний інтеграл:

.

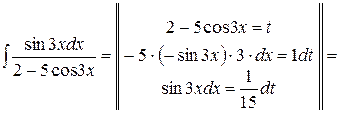
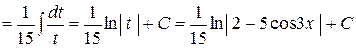5) Коли під коренем знаходиться вираз лінійний відносно якоїсь основної елементарної функції, тоді новою змінною зручно позначити весь корінь. Перетворення будуть містити один додатковий крок – піднесення до степеня, рівного степеню кореня.

.

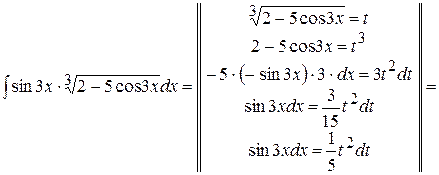
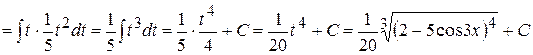6) Цього разу корінь квадратний, тому у другому рядку перетворень, пов'язаних із заміною змінної, треба обидві частини рівності піднести до квадрату:

.

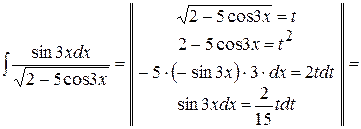
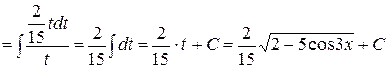7) У п’ятому прикладі під знаком кореня основна елементарна функція (у даному випадку 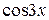) знаходиться у квадраті, тому за нову змінну доцільно обрати тільки саму функцію. З метою зведення без зайвих перетворень заданого інтеграла до табличного 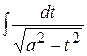доцільно підкореневий вираз представити так: 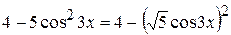. Тоді інтеграл обчислюють так:

.

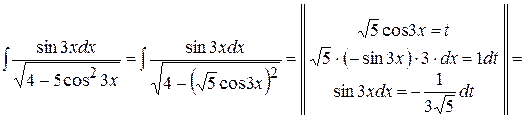
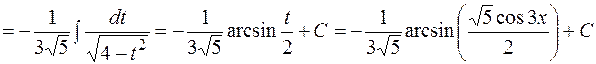8) Оскільки у таблиці інтегралів немає формули 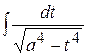, а наявна тільки 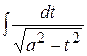, то саме до останньої треба звести заданий інтеграл. Для цього підкореневий вираз треба представити так: 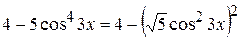. Тоді доцільною виявиться така заміна:

.

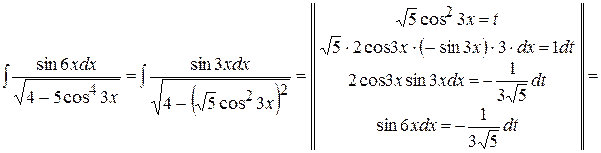
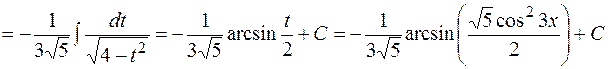На рис. 19.2 подана схема аналізу підінтегральних функцій на доцільність введення тієї чи іншої заміни.

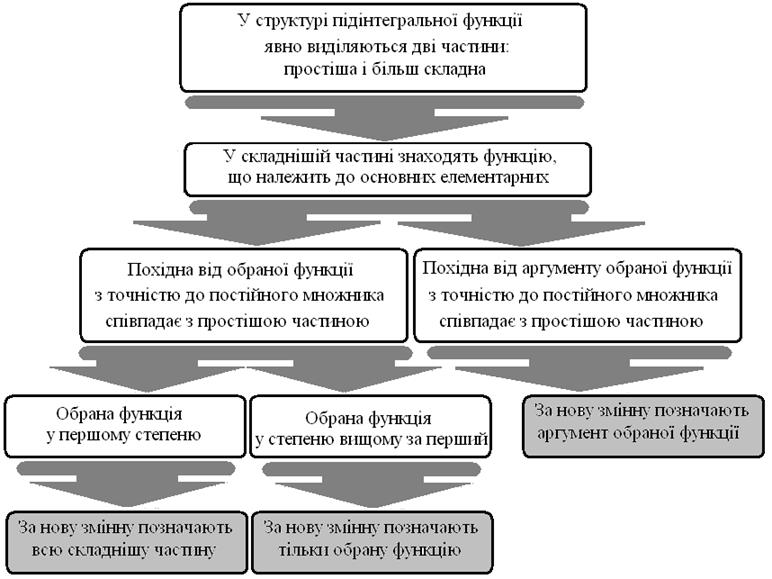
Рис. 19. 2. Спрощена схема аналізу підінтегральної функції при введенні нової змінної

Схема є спрощеною і стосується найбільш поширених ситуацій при застосуванні методу заміни змінної. Із неї існує багато виключень і уточнень, але нею варто користуватися на початку опанування теми: "Заміна змінної у невизначеному інтегралі".

Нагадаємо, що основними елементарними функціями є многочлен, раціональна, степенева, показникова, логарифмічна, всі тригонометричні функції та обернені до них.

Розглянемо виключення із запропонованої схеми, що зустрічаються найбільш часто.

Зауваження 19.5. У запропонованій схемі рекомендовано, якщо до більш складної частини одна із основних елементарних функцій входить у степеню, вищому за перший, то за нову змінну позначають тільки саму функцію (див. приклад 5). Але можливо виявиться доцільним за нову змінну позначити степінь обраної функції (див. приклад 6) з таким розрахунком, щоб заміна привела до табличного інтеграла (найчастіше це будуть інтеграли виду ; ; ; ).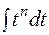

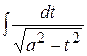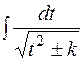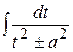Зауваження 19.6. При інтегруванні експоненціальної та показникової функцій треба звертати увагу на показники степенів цих функцій. Якщо більш проста та більш складна частини підінтегральної функції містять експоненціальну або показникову функції з однаковими показниками степенів, то найчастіше доцільною буде заміна, коли за нову змінну позначають усю більш складну частину. Якщо показник степеня у експоненціальної або показникової функції у більш складній частині удвічі більший, ніж у більш простій частині, то заміна повинна привести інтеграл до одного із видів ; ; .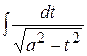

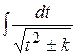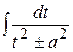Приклад 19.4. Обчислити невизначені інтеграли:

1) ;

2) ;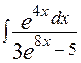

Розв’язання.

1) Очевидно, що більш простою частиною підінтегральної функції є чисельник 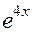, а більш складною – знаменник 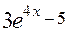. Показник степеня в обох випадках становить 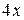, тому, у відповідності до зауваження, доцільною є заміна :

.

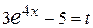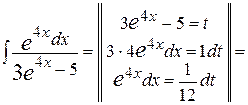
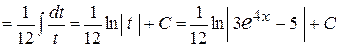2) У цьому прикладі також більш простою частиною підінтегральної функції є чисельник 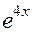, а більш складною – знаменник 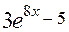, але показники степенів експоненціальних функцій є різними. Тому знаменник доцільно перетворити до вигляду 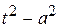. Остаточно отримаємо:

.

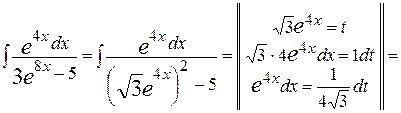
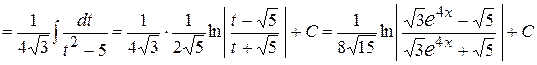Приклад 19.5. Довести за допомогою методу заміни змінної властивість 19.6 невизначеного інтеграла: якщо 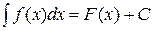, тоді

,

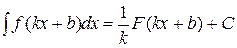де ; .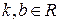

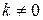Доведення. Позначимо 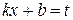. Тоді інтеграл обчислюється так:

.

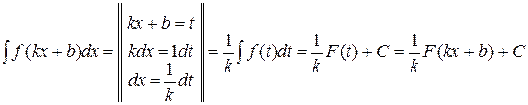Таким чином, тотожність (19.16) може бути доведена двома способами.