Доведення. І частина. За означенням первісної маємо, що
І частина. За означенням первісної маємо, що
 і і 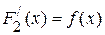
| (19.3) |
для будь-якого 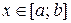 . Позначимо різницю функцій
. Позначимо різницю функцій 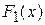 і
і 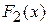 за
за 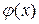 :
:
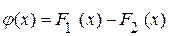 . .
|
Візьмемо похідну від обох частин останньої рівності:
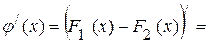
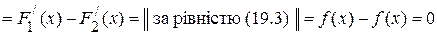 . .
| (19.4) |
Із рівності (19.4) маємо: якщо похідна функції дорівнює нулю 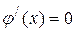 , тоді сама функція дорівнює сталій величині
, тоді сама функція дорівнює сталій величині 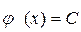 .
.
ІІ частина. Доведемо останнє твердження, крім того, знайдемо значення сталої величини С. Згадаємо теорему Лагранжа.
Теорема Лагранжа. Якщо функція 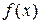 неперервна на відрізку
неперервна на відрізку 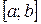 і диференційована в усіх внутрішніх точках цього відрізка, тоді всередині відрізка
і диференційована в усіх внутрішніх точках цього відрізка, тоді всередині відрізка 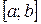 знайдеться щонайменше одна точка
знайдеться щонайменше одна точка 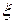
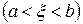 така, що виконується рівність:
така, що виконується рівність:
 . .
| (19.5) |
За припущеннями, зробленими у першій частині доведення, функція 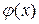 є неперервною і диференційованою, тобто вона задовольняє умовам теореми Лагранжа.
є неперервною і диференційованою, тобто вона задовольняє умовам теореми Лагранжа.
Тоді для будь-якого 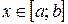 за теоремою Лагранжа всередині відрізка
за теоремою Лагранжа всередині відрізка 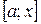 знайдеться щонайменше одна точка
знайдеться щонайменше одна точка 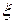
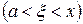 така, що виконується рівність, яка аналогічна рівності (19.5):
така, що виконується рівність, яка аналогічна рівності (19.5):
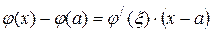 , ,
| (19.6) |
де 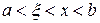 .
.
Із рівності (19.4) маємо 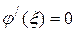 , тоді
, тоді
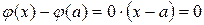 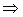
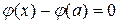 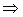
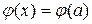 . .
|
Отже, функція 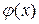 зберігає значення
зберігає значення 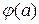 у всіх точках відрізка
у всіх точках відрізка 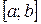 , тому
, тому 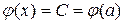 .
.
Наслідок 19.1. Якщо для функції 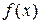 відомий вираз будь-якої її первісної
відомий вираз будь-якої її первісної 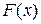 , тоді вираз іншої первісної цієї ж функції має вигляд
, тоді вираз іншої первісної цієї ж функції має вигляд 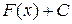 .
.
Дата добавления: 2015-08-14; просмотров: 578;
